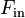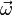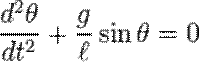Майкл, но вы же пишите , что это фиктивная сила. Получается , вы врали?
Вы , просто, не понимаете, в чем разница центробежной силы, действующей на человека, в целом, т.е на его цМ, который входит в уравнение движения, и на отдельные части тела. От этого все ваши беды.
Продолжим обучение
,
где 
— масса тела, 
— его ускорение относительно данной системы отсчета, 
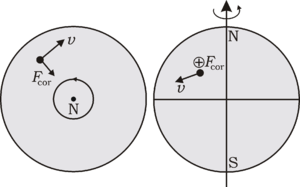
— реально действующая на тело сила, вызванная взаимодействием между телами, и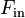 
— сила инерции, связанная с математическим преобразованием от инерциальной к неинерциальной системы отсчета. В равномерно вращающихся системах отсчета действуют две силы инерции: центробежная сила 
и сила Кориолиса 
. Следовательно, утверждения «Земля вращается вокруг своей оси» и «В системе отсчета, связанной с Землёй, действуют центробежная сила и сила Кориолиса» являются эквивалетными высказываниями, выраженными разными способами[1]. Поэтому экспериментальные доказательства вращения Земли сводятся к доказательству существования в связанной с ней системе отсчета этих двух сил инерции.
Направление силы Кориолиса на вращающейся Земле
Центробежная сила, действующая на тело массы , по модулю равна
,
где 
— угловая скорость вращения и 
— расстояние от оси вращения. Вектор этой силы лежит в плоскости оси вращения и направлен перпендикулярно от неё. Величина силы Кориолиса, действующей на частицу, движущуюся со скоростью 
относительно данной вращающейся системы отсчета, определяется выражением
,
где 
— угол между векторами скорости частицы и угловой скорости системы отсчета. Вектор этой силы направлен перпендикулярно обоим векторам 
и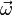 
вправо от скорости тела (определяется по правилу буравчика).
Эффекты центробежной силы
Зависимость ускорения свободного падения от географической широты. Эксперименты показывают, что ускорение свободного падения зависит от географической широты: чем ближе к полюсу, тем оно больше. Это объясняется действием центробежной силы. Во-первых, точки земной поверхности, расположенные на более высоких широтах, ближе к оси вращения и, следовательно, при приближении к полюсу расстояние от оси вращения уменьшается, доходя до нуля на полюсе. Во-вторых, с увеличением широты угол между вектором центробежной силы и плоскостью горизонта уменьшается, что приводит к уменьшению вертикальной компоненты центробежной силы.
Это явление было открыто в 1672 году, когда французский астроном Жан Рише, находясь в экспедиции в Африке, обнаружил, что у экватора маятниковые часы идут медленнее, чем в Париже. Ньютон вскоре объяснил это тем, что период колебаний маятника обратно пропорционален квадратному корню из ускорения свободного падения, которое уменьшается на экваторе из-за действия центробежной силы
"
"
В школьных учебниках законы Ньютона излагаются как истина в последней инстанции, хотя для их формулировки Ньютону пришлось ввести пять новых сущностей. Этими пятью сущностями являлись масса, как мера материи, сила гравитации, силы инерции, и инерциальные и гравитационные свойства массы. Все эти пять сущностей были введены Ad hoc, (ад хок от лат. ad hoc - к этому, для данного случая, для этой цели). Так, например, силы гравитации и гравитационные свойства масс были введены для объяснения падения тел на Землю и объяснения космических явлений, а центробежные силы инерции объясняли почему космические тела вращаются друг вокруг друга, а не падают друг на друга под действием гравитации. Соответственно, очередной задачей науки стало независимое подтверждение существования каждой из введенных сущностей. Самым существенным шагом в этом направлении был принцип эквивалентности, открытый в ходе эксперимента. Экспериментально было доказано, что центробежная сила действительно существует, что ее величина равна по величине центростремительной силе, вызывающей движение тела с ускорением, т.е. Fцс = Fцб.= MV2/R, где M, V и R масса, скорость и радиус круга вращения.
Давайте рассмотрим легко осуществимый эксперимент.
В этом эксперименте шарик, имеющий массу М, вращается на пружине. К нему присоединен динамометр, измеряющий силу натяжения пружины. В этой системе мы можем измерить орбитальную скорость движения шарика V, центростремительную Fцс и центробежную силу Fцб и радиус орбиты R.
В ходе эксперимента мы можем менять скорость вращения шарика на орбите и, соответственно, радиус отбиты. При увеличении скорости вращения увеличивается радиус орбиты, скорость движения шарика по орбите и возрастает центростремительная и центробежная силы.
Fцс = М V2/ R , Fцб = М V2/R
условие устойчивости Fцс= - Fцб
"
"Одним из таких физических феноменов является центробежная сила. Рассмотрим хорошо известную физическую систему – маятник (рис.6)
Дифференциальное уравнение математического маятника простое на вид, но оно не решается в виде элементарных функциях, так как во втором члене переменная ? входит в виде функции sin(?).
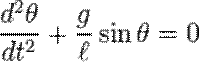(1)
Где, g – ускорение свободного падения, l – длина маятника, ? – угол отклонения маятника от вертикали.
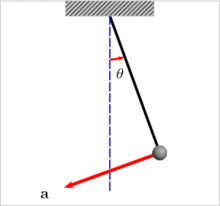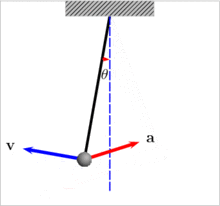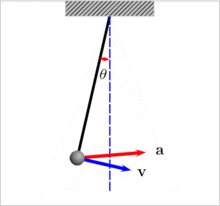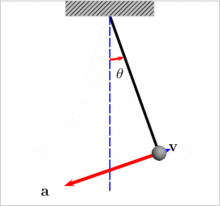
Рис.6. Маятник.
Не будь трения, маятник, раз отведенный от вертикали на угол ?, мог бы колебаться вечность. И для такого маятника справедливость закона сохранения энергии проявляется в том, что у него, отведенного от вертикали на 90 градусов, в нижней точке, соблюдается равенство кинетической энергии разнице потенциальных энергий между верхним и нижним положением маятника. Соотношение простое
П = К или M*g*h = M*v2/2 (2)
П – потенциальная энергия на максимальной высоте, К – кинетическая энергия на минимальной высоте, M – масса маятника, g – ускорение свободного падения, h – разница высот в положении маятника, v – скорость, с какой маятник «пролетает» нижнюю точку. Используя закон сохранения энергии и зная начальное отклонения маятника от вертикали, можно рассчитать скорость маятника в каждой точке.
При этом многие как-то забывают, что двигаясь по дуге окружности, маятник испытывает воздействие центробежной силы, которая является реальной внешней силой и указывает на соответствующую реакцию окружающей нас среды на изменение направления вектора скорости тела. Не пространства, а того, что заполняет все окружающее пространство. И имя этому одно – Эфир. Центробежную силу можно вычислить по формуле
Fц = М*v2/R или Fц = 2*K/R (3)
В формуле (2) Fц – центробежная сила, v – скорость перемещения массы M в вдоль искривлённой траектории, R - радиус кривизны траектории в точке, где скорость равна v. Можно даже утверждать, что на любые тела, даже те, которые двигаются по прямой, действуют центробежные силы. Так как радиус кривизны прямой линии равен бесконечности, то центробежная сила в этом случае равна нулю. Но если радиус кривизны траектории меньше бесконечности, то центробежная сила уже не равна нулю. Из формулы (3) следует, что центробежная сила присутсвует всегда, если тело движется по кривой траектории и обладается некой кинетической энергией К. Другой важной особенностью центробежной силы является то, что она всегда направлена перпендикулярно вектору скорости, в том же направлении, куда «смотрит» радиус-вектор R. А это означает, что центробежная сила не совершает работы над телом, которое двигается по изогнутой траектории, не участвует в энергетическом обмене между кинетической и потенциальной энергией тела, в данном случае, маятника.
Если подходить к центробежной силе с чисто математических позиций, то следует пересмотреть такое понятие как ускорение. Часто в учебниках как для школы, так и для институтов, под ускорением понимается первая производстная скорости по такому агрументу, как время. При этом предполагается, что скорость не меняет своего направления. Но, думаю, что под ускорением должна пониматься полная производная скорости. Изменение скорости во времени – это хорошо известное всем ускорение. А вот изменение скорости по осям координат – это уже и будет тем ускорением, которое мы воспринимаем как центробежную силу. И недостатком современной физической парадигмы является как раз то, что динамику процессов во времени ученые научились моделировать неплохо, но вот динамику отражения процесса внутри самого пространства, в самой среде, внутри которой осуществляется тот или иной процесс, физики представляют себе плохо. Этот пробел надо срочно ликвидировать. ОТО и СТО А.Эйнштейна смоделировать правильную картину окружающего нас мира не сможет. Это просто чистая кинематика, полигон для тренировки воображения, но реальность окружающего нас мира и виртуальность теорий Эйнштейна несовместимы.
Роль центробежной силы, как ответной реакции среды, особенная. Не нарушая энергетический баланс у самого тела, создавшего центробежную силу, сила эта оказывает силовое воздействие на само тело и тела, с которыми исследуемое, двигающееся по кривой линии, тело имеет те или иные связи. Пусть маятник в верхней точке закреплен с помощью оси или шарнира на более массивном теле, например, потолке или массивной балке. И при колебаниях маятник оказывает на точку подвеса уже воздействие не с силой, равной весу тела P = M*g, а сила эта, если отклонение ? не превышает 90 градусов, колеблется между неким минимумом P*cos(?) и максимумом P + Fц. Если мы отклоним маятник на 60 градусов, то при колебаниях такого маятника в самой нижней точке на шток и ось будет действать сила, равная 2*Р, при отклонении на 90 градусов – 3P, а при отклонении на 180 градусов – 5P. Это уже заслуживает самого пристального внимания, так как эту «составную» силу можно заставить выполнять работу. Если заставить маятник принудительно вращаться вокруг точки подвеса с угловой скоростью ?, то можно эту «составную» силу довести до очень больших значений, а выработку энергии можно будет поставить на промышленный поток.
При этом, создавая такую огромную силу, вращая маятник (эксцентрик) вокруг его оси (точки крепления), энергию придется тратить только на первоначальное раскручивание эксцентрика, а далее только на возмещение потерь энергии на трение. А вот сама центробежная сила дается нам Природой даром, как реакция среды (Эфира) на перемещение тела по криволинейной траектории. Чем меньше будет радиус кривизны траектории тела, тем больше будут центробежная сила. Теоретически центробежную силу можно сделать настолько большой, насколько это позволит реализовать прочность материалов, обеспечивающие и ограничивающие движение тела строго по заданной траектории.
Вот именно эта реакция среды и совершает ту работу, которую многие называют, кто сверх'единичной, кто свободной, а кто халявой. Но это только в том случае, если удастся силы реакции среды заставить это сделать. В этом как раз и состоит искусство и гениальность некоторых исследователей и изобретателей, многие из которых создают свои изобретения и совершают великие открытия, опираясь исключительно на свою интуицию и уверенность в своей правоте. Часто такие гении даже не знают, где можно применить их изобретение или открытие. Например, когда Фарадея спросили, где можно использовать его неказистые электромоторы, то он высказал то, что первым пришло в его голову – в игрушках.
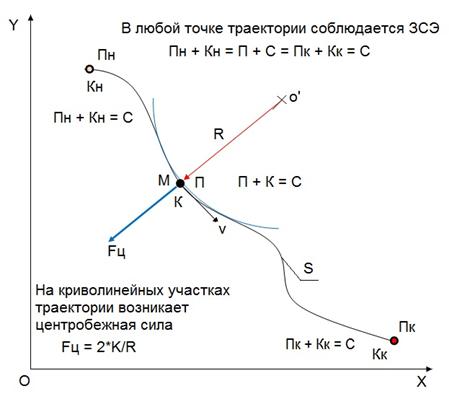
Рис.7. Закономерности при движении тела по криволинейной траектории.
Отразим на рис.7. известные законы физики. Пусть тело М перемещается по траектории S из начальной верхней точке к конечной нижней точке. В начальном положении она обладает потенциальной Пн и кинетической энергией Кн, в конечной точке тело уже будет обладать потенциальной энергией Пк и кинетической энергией Кк. В некой промежуточной точке тело М обладает потенциальной энергией П и кинетической энергией К. С соотвествии с законом сохранения энергии Пн + Кн = П + К = Пк + Кк = С. С – это сумма потенциальной и кинетической энергии, которая согласно ЗСЭ остается постоянной вдоль всей траектории S. Но траектория S криволинейная, поэтому кривизна трактории на некоторых участках не будет равна нулю. Радиус кривизны в каждой точке траектории S можно найти либо по формулам, либо численным методом, либо просто измерить. И если радиус R кривизны траектории в точке, где находится тело М, не равен нулю, то на тело М со стороны среды действует центробежная сила Fц, величину которой можно вычислить по формуле (3) – Fц = 2*К/R.
О законе сохранения энергии все знают, а некоторые яростно защищают, если создавший интересный аппарат изобретатель начинает утверждать, что этот аппарат не подчиняется закону сохранения энергии. Считаю, что закон сохранения энергии (ЗСЭ) при любом взаимодействии соблюдается всегда. Но с другой стороны многие просто забывают о таком феномене, как центробежная сила.
Эта сила всегда направлена в том же направление, что и радиус кривизны в данной точке, одновременно она составляет прямой угол с мгновенной скоростью, т.е., с касательной к траектории в точке нахождения тела M. По модулю центробежная сила Fц может быть маленькой, но может быть запредельно большой. И когда сила Fц оказывается большой, то это может сопровождаться некими эффектами, которые будут оцениваться (и не без основания) в форме сверх'единичного эффекта. Как производная скорости по координатам центробежная сила не подчиняется законам относительности, где определяющим аргументами являются время и скорость. Она, если не неизменна в любой системе координат, то по крайней мере в любой системе координат будет иметь конечное значение, никогда не превращаясь в ноль. И в любом случае на «перелив» кинетической энергии в потенциальную и обратно вдоль траектории тела центробежная сила не влияет.
Нами уже было отмечено, что колебания простого маятника сопровождаются формированием центробежной силы, величина которой в крайних положениях равна нулю, так как равна нулю скорость груза, а значит и кинетическая энергия, а в самой нижней точке (точке устойчивого равновесия) центробежная сила может достигать заметной величины. Если максимальный угол отклонения маятника составляет 60 градусов, то в нижней точке к весу P добавляется Fц, равная весу тела P. Если угол отклонения составит 90 градусов, то цетробежная сила в нижней точке будет равна 2*P, если угол отклонения сотавит 180 градусов, то центробежная сила в самой нижней точке будет равна 4*P.
Следовательно, даже маятник с малой амплитудой колебаний воздействует на точку крепления стержня и сам стержень с переменной силой. И если мы исследуем только сам маятник, ось которого жестко связана с массивным телом, таким как Земля, то центробежную силу можно не учитывать, если нам нужно знать только кинематические характеристики маятника. Но если нам необходимо рассчитать диаметр стержня или троса, чтобы он не оборвался при колебаниях, то учитавать центробежную силу уже надо. Или если маятник используется как источник переменной силы в таком маятнике, как маятник Милковича, то также необходимо не просто учитывать наличие переменной центробежной силы, но также уметь правильно расчитать силовые и мощностные характеристики всей конструкции, да еще при этом найти в себе силы и волю, чтобы дать отпор борцам с лженаукой.
"
Сообщение отредактировал Maykl: 23 December 2015 - 11:31
