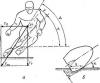
Alex_63, скажи, как можно так долго не понимать, что мы работаем в инерциальной системе отсчета и в этой системе нет ЦБС , действующей на лыжника. Уже и Вики цитировал подробно, и академика и чертежи рисовал. Я пользуюсь академическими определениями и знаниями. Либо ты их разделяешь, либо нет. Если не разделяешь, то ты не разделяешь логику Ньютона, а создаешь свои теории, исходя из интуитивного представления. А интуиция может подводить.. Без общего понятийного аппарат нет смысла дискутировать.
Если по существу, то я расчетами показал, что при определенных скоростях сила реакции склона проходит ниже ЦМ в инерциальной системе отсчета, а в неинерциальной равнодействующая силы тяжести и ЦБС выходит за пределы опоры, вопреки ошибочным представлениям Майкла. Это и требовалось - лишний раз доказать правоту автора обсуждаемой статьи. Но об этом он написал, аж, 3 года назад.
Поскольку ты тоже согласен, что равнодействующая пройдет ниже цМ, то давай закроем дискуссию.
ИНЕРЦИЯ -это не сила, это свойство сохранять скорость
Степаныч, мне очень жаль что все таки придется разоблачить и тебя и работу Ника. Хотя мне все это время очень не хотелось![]()
УЧЕБНИК ДЛЯ ВУЗОВ.
В.И. ДУБРОВСКИЙ, В.Н. ФЕДОРОВА
БИОМЕХАНИКА
Рекомендовано Государственным комитетом Российской Федерации по физической культуре, спорту и туризму в качестве учебника для средних и высших, учебных, заведений по физической культуре
Глава 8 НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА 8.1. Сила инерции. Принцип Д'Аламбера
В ряде случаев возникает необходимость описать движение, покой или равновесие тела, находящегося в неинерциальной системе отсчета. Например, требуется выяснить какие проблемы могут возникнуть у человека, находящегося в кабине космического корабля. Французский физик Д'Аламбер сформулировал простой принцип, позволяющий отвечать на вопросы о поведении тела в неинерциальной системе. Рассмотрим тело, которое находится в неинерциальной системе, движущейся относительно инерциальной системы с ускорением ас.
Векторная величина, равная произведению массы тела на ускорение системы и направленная в сторону, противоположную ускорению системы, называется силой инерции:
Fи=-m?ac. (8.1)
Сила инерции не является реальной силой, так как она не действует со стороны какого либо тела. Однако в неинерциальной системе ее можно (и нужно!) рассматривать, как обычную силу. При этом можно «забыть» о том, что система неинерциальна.
Д'Аламбер установил, что если ко всем реальным силам (действующим со стороны других тел) добавить силу инерции, то в неинерциальной системе можно использовать все законы и формулы, которые справедливы для инерциальных систем.
Далее
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ТЕОРЕТИЧЕСКИХ ОСНОВ ФИЗИЧЕСКОЙ КУЛЬТУРЫ
Система отсчета —условно выбранное твердое тело, по отношению к которому определяют положение других тел в разные моменты времени.
В мире не существует абсолютно неподвижных тел, все тела движутся. Но одни из них движутся так, что изменения их скорости (ускорения) несущественны для решения данной задачи и ими можно пренебречь, — это инерциальные системы отсчета. Такие тела — Земля и тела, связанные с нею неподвижно (дорожка, лыжня, гимнастический снаряд). В подобной системе покоящиеся тела не испытывают действия сил; значит, в ней ни одно движение не начинается без действия силы.
Другие тела движутся с ускорениями, которые существенно влияют на решение данной задачи, — это неинерциальные системы отсчета (скользящая лыжа, раскачивающиеся кольца)1. В таких случаях способы расчета и объяснения особенностей движений уже иные, что надо обязательно учитывать.
А это ответы для подготовки к экзамену по дисциплине
«Биомеханика двигательной деятельности»
Наблюдая движения человека, можно заметить, что многие их особенности все время изменяются. Изменяется положение звеньев тела, скорости движения и многое другое. Особенности (или признаки) движения позволяют разделить сложное движение на составные части, заметить, как они влияют одна на другую, как помогают достичь цели. Для этого и изучают характеристики движений человека.
Характеристики движений человека - это те особенности, или признаки, по которым движения различаются между собой.
Различают качественные и количественные характеристики.
Качественные характеристики - характеристики, описываемые только словами и не имеющие точной количественной меры (например: напряженно, свободно, плавно, мягко и др.).
Количественные характеристики - характеристики, которые измеряют или вычисляют, они имеют количественную меру.
Педагогу при проведении урока нечем и некогда измерять и регистрировать количественные характеристики. Ему приходится пользоваться качественными характеристиками, он проводит качественный биомеханический анализ движений каждого ученика.
Изучая движения с помощью измерительной и записывающей аппаратуры, получают количественные характеристики. Их обрабатывают, проводят вычисления для количественного биомеханического анализа. Конечно, затем должен следовать и качественный анализ, чтобы понять законы движения и использовать их в физическом воспитании. Хорошо владея навыками количественного анализа, в повседневной практической работе можно с успехом пользоваться только качественным анализом.
Вся сложность взаимосвязи характеристик, используемых для изучения движений человека, отражена в схеме.
Из нее видно, что наиболее важными являются те из них, которые характеризуют изменения положения тела и движения. К ним относятся кинематические и динамические характеристики. При этом следует отметить тот факт, что движения человека и предметов, перемещаемых им, можно заметить и измерить, только сравнивая их положения с положением выбранного для сравнения тела (тело отсчета ) . Поэтому все движения человека в биомеханике рассматриваются как относительные .
Движение выражается в изменении с течением времени взаимного положения тел. Его можно наблюдать и отсчитывать только относительно других реальных тел (например, при прыжках в длину - относительно бруска) или условных (например, в старте яхт - относительно линии створа) .
В зависимости от условий задачи, стоящей при изучении двигательного действия, выбирается та или иная система отсчета . Принято выделять:
- инерциальную систему отсчета (Земля, дорожка, лыжня) - движения их в данной системе незаметны при измерениях, т.е. изменениями скорости, ускорениями при решении данной задачи можно пренебречь;
- неинерциальная система отсчета - движущееся тело (скользящая лыжа, раскачивающиеся кольца), движение которого происходит с заметным ускорением, существенно влияющим на отсчет расстояния;
Далее. Снова вернемся к УЧЕБНИКу ДЛЯ ВУЗОВ.
В.И. ДУБРОВСКИЙ, В.Н. ФЕДОРОВА
БИОМЕХАНИКА
Рекомендовано Государственным комитетом Российской Федерации по физической культуре, спорту и туризму в качестве учебника для средних и высших, учебных, заведений по физической культуре
5.3. Законы Ньютона для произвольного тела. Поступательное движение
Покажем, как понятие центра масс используется в законах Ньютона.
На каждую материальную точку, входящую в состав тела, действуют силы как со стороны других тел — внешние силы, так и со стороны остальных точек самого тела — внутренние силы. Например, для падающего тела внешними являются сила тяжести и сила сопротивления воздуха, а внутренними являются силы взаимодействия между молекулами. Обозначим Fi сумму всех сил, действующих на точку с номером i, и запишем второй закон Ньютона для всех точек:
F1 = т1?а1
F2 = т2?а2,
……………
Fп= тn?аn,
Сложив все равенства, получим:
F1+F2+... + Fn=m1?a1+m2?a2+... + mn?an. (5.5)
Слева стоит сумма всех сил, действующих на все точки тела. Среди них есть как внешние, так и внутренние силы. В соответствие с третьим законом Ньютона сумма всех внутренних, сил равна нулю (силы, с которыми материальные точки действуют друг на друга, равны по величине и противоположны по направлению и при сложении дают ноль). Поэтому сумма всех сил в равенстве (5.5) равна сумме внешних сил:
F1+F2+... + Fn = Fвн
В правой части равенства (5.5) стоит числитель формулы (5.3). Поэтому
m1?а1 + т2?а2 + ... + тп ? ап = (m1 + т2 + ... + тп) ?а = т?а.
С учетом этого равенство (5.5) принимает следующий вид:
F=т?а .. (5.6)
Или![]()
Соотношение (5.7) является вторым законом Ньютона для произвольного тела.
В инерциальной системе отсчета ускорение центра масс тела равно отношению суммы внешних сил к массе тела.
Первый и третий законы Ньютона для произвольного тела обобщаются следующим образом.
Существует система отсчета, относительно которой центр масс тела движется равномерно и прямолинейно или сохраняет состояние покоя, если на него не действуют другие тела. Такая система называется инерциальной.
Любые взаимодействующие тела действуют друг на друга с силой, одинаковой по величине и противоположной по направлению: F = —F
Инерциальная система отсчёта сама должна либо покоиться, либо равномерно и прямолинейно двигаться.
Всё остальное - неинерциальные системы.
Любая система, движущаяся с ускорением относительно инерциальной системы отсчёта , является неинерциальной.
Далее![]()
Степаныч, если тебе действительно захочется рассчитать силы которые действуют на горнолыжника в повороте, то это минимум должно выглядеть вот так. И обрати внимание в какой системе отсчета производились вычисления
8.5. Применение законов динамики для анализа движений спортсменов
Разберем некоторые примеры, показывающие, каким образом законы динамики применяются -для анализа сложных движений и вычисления сил, нагружающих суставы, сухожилия и мышцы.
На рис. 8.8. показан стартующий бегун. На него действуют сила тяжести mg и реакция опоры R, сообщающие центру масс бегуна ускорение а.
Рис. 8.8. Силы, действующие на тело спринтера при отталкивании во время старта
Воспользуемся неинерциальной системой отсчета, связанной с центром масс. В этой системе центр масс покоится. Согласно принципу Д,Аламбера к реальным силам следует добавить фиктивную силу инерции FИ = -т?а и записать условие покоя: ![]()
В проекциях на координатные оси это равенство запишется в виде системы двух уравнений:![]()
где Rx, Ry — составляющие реакции опоры; аy и ах — вертикальная и горизонтальная составляющие ускорения центра масс в момент старта.
Эти уравнения можно использовать для решения двух задач:
• зная силы, действующие на тело, описать движение центра масс;
• зная ускорение тела (используя различные способы регистрации, например, киносъемку), определить вызвавшие его силы.
Вычислим силу тяги мышц fm, нагружающих ахиллово сухожилие при старте бегуна. На рис. 8.9 показаны стопа и действующие на нее силы.
Это реакция опоры R, сила тяжести mcT?g, сила тяги мышц Fm и сила, нагружающая голеностопный сустав, F. Кроме того, на стопу действуют силы пассивного сопротивления, связанные с деформацией соединительных тканей и с силой трения в суставе.
Рис. 8.9. Силы, действующие на стопу спортсмена при отталкивании
Обозначим ускорение голеностопного сустава аст и воспользуемся связанной с ним неинерциальной системой отсчета. В этой системе сустав неподвижен, а стопа вращается вокруг него с некоторым угловым ускорением ?. Согласно принципу Д'Аламбера к реальным силам следует добавить фиктивную силу инерции Fи = —т? аст и записать условие вращения:![]()
где mст, Iст — масса и момент инерции стопы (относительно голеностопного сустава); Мc, — момент сил пассивного сопротивления; Мм — момент силы тяги мышц (Fм), нагружающих ахиллово сухожилие; hх, hу, h1, h2 — плечи сил.
Проанализируем левую часть этого уравнения. Сила тяжести (mст?g) и сила инерции (mстаст), действующие на стопу, малы по сравнению с силами реакции опоры (Rx и Ry ), а их плечи (h2 и h2) меньше плеч сил реакции опоры(hx и hy). Поэтому моментами этих сил (—mn?g?h2 и mn?aст?h1 ) можно пренебречь. Момент сил пассивного сопротивления в суставе С/И.) также незначителен по сравнению с моментами сил реакции опоры.
Правую часть уравнения можно принять равной нулю, поскольку согласно расчетам и измерениям, произведение момента инерции стопы; на ее угловое ускорение (Iст ??ст) мало по сравнению с основными слагаемыми левой части. Поэтому уравнение (8.10) упрощается:![]()
Отсюда получаем соотношение для момента силы тяги мышц:![]()
Момент силы тяги мышц равен произведению силы на плечо:![]()
а составляющие реакции опоры определяются системой (8.9):![]()
Подставив эти выражения в (8.11), получим:![]()
Отсюда находим формулу для расчета приближенного значения силы тяги мышц, нагружающих ахиллово сухожилие:
Вычислим ориентировочное значение этой силы. Для взрослого человека можно принять т = 70 кг, hy =12 см, hx =10 см, h3 = 6 см. Измеренные значения составляющих ускорения центра масс равны а ![]() 1,5g, a
1,5g, a![]() g. Подставив эти значения в (8.12) получим:
g. Подставив эти значения в (8.12) получим:![]()
Полученное значение близко к максимально допустимой нагрузке для ахиллова сухожилия, которая составляет примерно 5000 Н.
Проведя аналогичные расчеты, можно получить значение для силы F, которой нагружен голеностопный сустав. В данном случае получается значение близкое 3?mg.
![]()
![]()
![]()
![]()
Сообщение отредактировал Maykl: 16 November 2015 - 02:43