miron0ff

Андрей Ста сказал(а) 13 Ноя 2022 - 16:15:

Когда лыжник стоит на склоне, то правильная стойка не является проблемой. Проблема - это правильная стойка в момент входа в очередной поворот. Если предыдущий поворот происходил на более-менее крутом склоне.
 

rzuev сказал(а) 07 Ноя 2022 - 14:08:

что есть ангуляция, которая по-твоему миф?

Определение ангуляции через изгибы в проекции тела на соответствующую плоскость  само по себе не имеет особого значения. Имеет значение угол ангуляции и его изменение. Угол ангуляции это угол на который отличаются угол закантовки лыж и угол инклинации. Только этот угол влияет на динамику поворота и на врезание лыж. Угол ангуляции может быть создан множеством способов. Не только изгибами тела. Например опорой на палку при повороте. Например соответствующей амортизацией  при падении прямого тела в поворот в самом начале поворота. Но даже при существенных изгибах тела угла ангуляции может и не быть.
 

Alex_63 сказал(а) 07 Ноя 2022 - 13:15:

Да что бы лыжа проскальзовала надо Fr повернуит по часовой ниже Fn или на крайняк совместить с ней.

Именно так. Автор как раз совместил эти две силы в итоге. После нескольких страниц воды.

В статье рассматривают чисто геометрическую схему сил. В этом случае соотношение между F_c и N будет рано тангенсу пси (это угол закантовки лыжи), это чисто геометрический эффект и следствие того, мы считаем что лыжа находится в равновесии. Так как F_c=F_rsin(Ψ) а N=F_rcos(Ψ). Но это не значит, что лыжа будет проскальзывать. А если и будет проскальзывать, то совсем не обязательно, что коэффициент эффективного трения будет равен тангенсу угла закантовки, или даже пропорционален этому тангенсу. Но если лыжа не проскальзывает то соотношение между F_c и N будет рано тангенсу некоторого угла. Но этот тангенс нельзя называть коэффициентом трения.
 

mcureenab сказал(а) 06 Ноя 2022 - 15:54:

Лыжник всегда вдавливает лыжу в склон, но не всегда лыжа проскальзывает боком. Вообще, если достаточно сильно давить по касательной к поверхности снега (против силы F_c), лыжа начнёт срезать снег - проскальзывать боком.

 

Отработка движется от канта вверх по пунктирным стрелкам и создаёт силу трения F_f которая стремится вытолкнуть лыжу из снега. Если вес лыжника равен -F_r лыжа будет срезать слой снега с постоянным заглублением. Понятно, что срезать снег лыжа может, если давление больше предела прочности. В противном случае лыжа просто упрётся в снег и получится карвинг.

Лемастер сформулировал простой критерий того, что значит "достаточно сильно давить по касательной к поверхности снега" для того чтобы лыжа начала проскальзывать. На схеме как раз изображен тот случай когда, согласно Лемастеру, лыжа не будет проскальзывать. Что касается силы трения, то она будет незначительной, так как коэффициент трения между лыжей и снегом равен примерно 0.04. Угол тау на схеме тогда должен быть изображен как 2 градуса, и сила трения F_f  должна быть изображена на этой схеме примерно как точка. Но если бокового проскальзывания нет, то нет и движения отработки и, соответственно, нет и силы трения F_f. При таком направлении F_r лыжа будет углубляться в снег в направлении этой силы и не будет проскальзывать вы боковом направлении. Это было установлено экспериментально.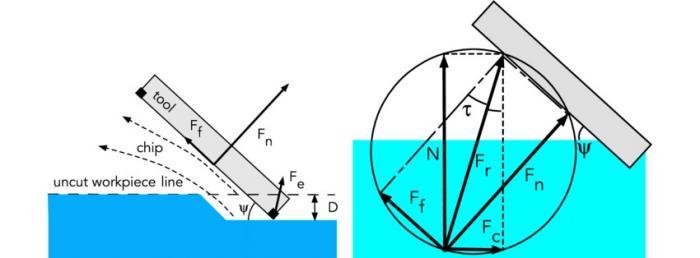

Если же рассматривать проскальзывание, тогда, согласно Лемастеру, лыжа начинает выскальзывать из канавки. Но в этом случае представленная схема выглядит неактуальной. И неактуальными будут все оценки, сделанные на основании этой схемы.

mcureenab сказал(а) 05 Ноя 2022 - 20:01:

Тут чел исследует резание снега.

 

https://www.research...now-and-ice.pdf

 

Теория плохо согласуется с наблюдениями, но общий вывод, что эффективный коэффициент трения растёт как тангенс угла закантовки, т.е. до бесконечности, наблюдается. При 45гр получаем эффективный коэффициент трения = 1, и перегрузку g. И всё это в режиме резания, когда прочность снега меньше давления на него.

Здесь явное недоразумение. На схеме изображен случай резания. По крайней мере в этом был уверен Лемастер.

Сила которая действует на лыжу со стороны лыжника - Fr - вдавливает лыжу в склон. Лыжа будет врезаться в склон и не будет проскальзывать. Так говорил Лемастер. Никакого проскальзывания лыжи не будет. С Лемастером трудно не согласиться в этом вопросе. А автор просто не разобрался в теме и запутался в стрелочках.
 

Гойко Митич сказал(а) 29 Сен 2021 - 07:48:

Как может   момент, создаваемый силой тяжести,  быть уравновешен центробежной силой, которой нет  в изначальном уравнении движения? Ничто там не уравновешено, ни силы, ни моменты

То, что там будут внешне похожие зависимости, а по другому и быть не может, не означает возникновение ЦБС. 

Можете вывести тангенциальную зависимость угла наклона  от скорости и радиуса поворота в инерциальной системе

 

Уравнение моментов в инерциальной системе отсчёта, когда моменты сил вычисляются относительно движущейся оси, выглядит сложнее, чем уравнение моментов относительно неподвижной оси. Я имею ввиду уравнение для производной момента импульса лыжника относительно оси лыжи в инерциальной системе отсчета. В данном случае ось лыжи, относительно которой вы составляете уравнение моментов движется в инерциальной системе отсчета. Если это движение происходит с ускорением и с вращением оси лыжи относительно склона, то такое движение изменит уравнение моментов. Вас интересует как будет изменяться угол наклона опорной линии при движении лыжника в инерциальной системе отсчета. В уравнениии моментов, которое описывает изменение угла наклона в зависимости от времени, будет 2 слагаемых, которые определяют это изменение. Это момент силы тяжести относительно оси лыжи и слагаемое, которое выглядит в точности как момент силы инерции относительно оси лыжи. Можете говорить об этом слагаемом что угодно. Например, что это момент фиктивной силы, которой не бывает в природе, или что-то другое, но от этого уравнение не изменится. Когда момент силы тяжести будет уравновешен моментом этой, если хотите, фиктивной силы, то угол наклона опорной линии меняться не будет. Если эти моменты не уравновешены, то угол будет изменяться. Вы и сами легко сможете вывести тангенциальную зависимость.

Alex62 сказал(а) 26 Сен 2021 - 20:28:

 Для чего в фазе перекантовки удобнее оказаться в задней стойке, чтобы с задников получить импульс на продвижение тела вперёд лыж на лпс и грузануть недолго передок. 

График показывает совсем не то, что вы утверждаете. Импульс на продвижение тела вперед полностью возникает тогда, когда давления, как вы говорите, нет. В середине фазы сопряжения. Также интересен вопрос что именно гасит импульс по продвижению тела назад в конце цикла поворота. По вашей логике в этот момент должны быть загружены носы лыж. Но давление на склон равно нулю.

Antry сказал(а) 23 Окт 2020 - 18:18:

Раребёрд вроде бы является соавтором широко известной в узких кругах статьи Леготина и Ривлина про базовую механику гл поворота, в которой движение рассматривается относительно склона и написаны 3 основополагающих уравнения движения гл-ка как мат точки. Другое дело, что там вкралась ошибка в решении этих уравнений, но это не так важно, хоть и досадно.

Дело в том, что получаемые в результате решения каких-то уравнений какие-то цифры никак не повлияют на наше катание, но понимание правильной постановки задачи (теории) может избавить от множества заблуждений и направить дискуссию в правильное русло. Хорошая теория очень практична.

В этих постановочных простых  уравнениях учитывается не только уклон склона и положение лыжника относительно этого уклона (и соответственно описывается формулами изменение нагрузки на лыжи в повороте до и после лпс), но и заложена возможность учёта "вертикальной работы", т.е. перемещения цт в вертикальном направлении или в направлении перпендикулярно к склону.

А так же очень важно, что учитывается трение - то, чем собственно всех больше всего и интересует при спуске на гл.

Нагрузка на лыжи увеличивается от "вертикальной работы". Важно опускать и поднимать цт в апексе поворота в стороне от лыж. (расстояние между цт и лыжами в процессе поворота остаётся практически постоянным). 

Эти движения тоже заложены в вышеописанных уравнениях и можно задать какой-то закон  вертикальных перемещений, и получить много разных цифр,  но для практического нашего  катания эти цифры не имеют никакого значения.  Мы же не роботы.

 

Мне интересно другое.

Я предполагаю, что статья Леготина и Ривлина верна и уравнения движения относительно неподвижной системы координат грамотно описывают процесс перемещения мат. точки по некоторой сложной траектории, перемещающейся вдоль наклонной плоскости и кроме того имеющей дополнительное перемещение перпендикулярно этой плоскости по некоторому закону.

 

Мне непонятно, как  после соавторства с этой статьёй можно одновременно делать ролики на основании псевдонаучной ахинеи Каниовского про "некоторые аспекты карвингового поворота"?

Зачем Вам это нужно?  Вы же очень хорошо катаете и не сомневаюсь, очень грамотно тренируете. 

Книга Каниовского про катание на лыжах замечательная, хорошо написана, полезная и интересная для начинающих. 

Главу про "теорию" я думаю что 99% читающих пропускают за ненадобностью.

И правильно делают. Плохая теория не практична.

Зачем Вы используете самую неудачную ("научную") главу из его книги для своих роликов ?

Статья Ривлина и Леготина является совершенной ахинеей с научной точки зрения. Леготин признал ошибочность этого опуса.

Но следует сказать спасибо Ривлину, что он рекламирует работу Каниовского.

Antry сказал(а) 25 Окт 2020 - 22:36:

Принципиальная ошибка заключается в том, что движущийся по дуге лыжник заменяется неподвижным альпинистом, упирающимся под углом к склону. Между ними есть существенная разница, хотя некоторые люди настолько одарены, что 

Коллега, вы пишете эту глупость снова и снова. У Каниовского нет никакой ошибки. Ошибка есть у вас. Эта ваша застарелая ошибка связана с абсолютным вашим непониманием физики.

Лыжник неподвижен в системе отсчета связанной с его лыжами. Но эта система отсчета неинерциальная и в этой системе отсчета возникает сила инерции, которую может измерить в этой системе  любой неподвижный относительно этой системы наблюдатель , пользуясь объективными методами.

mcureenab сказал(а) 20 Мар 2020 - 12:00:

Рано ты с практики сбежал.

 

Откуда тут g образовалась [r, mg]?

 

[dr/dt, mv] = 0

Интересно. Дискуссия на высоком научном уровне.

Подскажу вам, коллега, так как продолжения дискуссии я не увидел, что первое векторное произведение - это момент силы тяжести.

Второе векторное произведение не равно нулю в общем случае.

Гойко Митич сказал(а) 30 Сен 2020 - 09:37:

Есть такое понятие, как врезающая сила. без которой поворот  не состоится. Лыжи будут проскальзывать. А врезающую силу обеспечивает ангуляция. И это причина.

Коллега, советую вам ознакомиться с интересной позицией Полинковского по этому вопросу.

Он говорит, что врезающая сила обеспечивается наличием так называемой безопорной фазы в цикле поворота.

Следовательно, ангуляция не является причиной возникновения врезающей силы.

Oлена сказал(а) 28 Сен 2020 - 20:13:

Вот этот момент меня как инструктора очень интересует!

Если Вас не затруднит определить "тайминг" по терминологии ГМ ( или tempismo esecutivo) включения соответствующих мышц  в определённой фазе поворота с точки зрения динамики этой сложной системы (которую с Ваших же слов описать математически достаточно проблематично) то мы сможем продвинуться немного вперёд в понимании процесса. Или же

 с грустью приходим к тому что эмпирически нам проще определить когда включать действие определённых мышц.

Советую вам посмотреть недавнюю беседу Полинковского примерно на эту тему.

Основной посыл - чтобы обеспечить достаточную вертикальную составляющую веса лыжника, лыжнику необходимо часть времени не оказывать давления на склон совсем.

Чем больше нужная вертикальная составляющая веса, тем дольше в цикле поворота лыжник не должен оказывать давления на склон.

Здесь можно добавить, что задачей лыжника является более-менее равномерное "размазывание" избыточного вертикального, по отношению к поверхности склона, импульса по активной фазе резания дуги поворота.

Полинковский говорит об обеспечении максимального давлениея в апексе поворота.

Но как -то нужно "дотащить" этот избыточный вертикальный импульс до апекса и при этом обеспечить раннее врезание лыж.

В этом - основной вопрос.

Можно взять за основу аналогию с приземлением прыгуна после прыжка вверх - цикл амортизации, который сопровождается относительно растянутым замедлением движения центра масс к земле.

Проблема в том, что лыжник "падает боком на склон" в начале дуги.

Особенно это относится к квалифицированным лыжникам.

Попробуйте поразмышлять о том какими конкретными действиями этого можно добиться.

Maykl сказал(а) 28 Сен 2020 - 19:39:

Тут тоже вроде все доступно для понимания)

 

"ЦЕНТР ДАВЛЕНИЯ

 ЦД в целом физически не зависим от ОЦМ. 

Очень грамотное разъяснение для иллюстрации вопроса Гойко Митича.

Его вопрос был по сути.

Но конкретно вы, очевидно, не очень понимаете то, что цитируете.

Maykl сказал(а) 27 Сен 2020 - 21:33:

Перенос с двух в одну увеличивает давление. Так что все норм, если про физику. А то  закидаю ссылками на биомеханику и Центр масс

Для врезания важен угол, под которым направлено давление на лыжу, а не величина этого давления.

Цитаты, которые вы приводите написаны людьми, которые их высасывали из пальца.

Все их воззрения противоречат экспериментальным данным, которые получены при исследовании проездов очень квалифицированных лыжников.

Вы, да и 99,99999% участников форумов этого сайта к таковым не относятся.

Maykl сказал(а) 14 Сен 2020 - 11:07:

если взять лыжи одной длины и радиуса н от с разным распределением продольной и торсионной жёсткости, то получим совершенно разную Аля критическую скорость просто тупо возможности этой самой лыжи держать скорость без срыва на критических углах. В итоге все эти критические скорости просто конь в вакууме. На практике это выглядит так что лыжу с неравномерным распределением жёсткости начинает просто тупо срывать с дуги, хотя возможных условий для стационарной дуги в равновесном состоянии для лыжи с более равномерным распределением жёсткости ещё предостаточно.

Каниовский дал критерий, который выполняется, если реализуется резаный поворот. Критическая скорость не имеет отношения к критическому углу закантовки.

Эта скорость расчитывается из гипотетического предположения, что лыжник может позволить себе углы закантовки вплоть до 90 градусов. То есть на критической скорости лыжник не сможет сохранить равновесия в дуге даже при 90 градусной закантовке.

При небольших углах закантовки и соответствующем состоянии склона практически любая современная карвинговая лыжа способна ехать по резаной дуге без срыва.

Для такого поворота скорость движения при которой дуга перестанет быть стационарной будет меньше критической скорости для данного радиуса лыж.

Вы ставите совсем другой вопрос, которым Каниовский не занимался.