Legotin_S

Ну  это Вы загнули.На чем основан Ваш вывод?.. Проскальзывание , конечно, используется для сброса избыточной скорости. Это когда эта скорость совсем уж избыточная. А скорость 40-45 км/ч является типичной для слаломистов высокого уровня.  И при этой скорости они едут, именно, резаной дугой, иначе, проскальзывание не сможет обеспечить нужную величину центростремительной силы для малого радиуса поворота. Собственно по следам и видно, что никакого проскальзывания нет. ПО Вашей теории они не могут ехать при таких скоростях по таким радиусам

Я не помню, относительно чего я говорил про скорость. вероятно, про Вашу равновесную дугу. Равновесная дуга определенного радиуса, действительно. проходится быстрее при отсутствии ангуляции

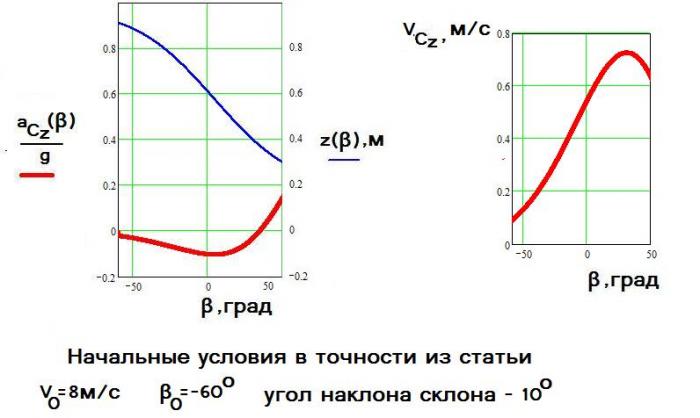
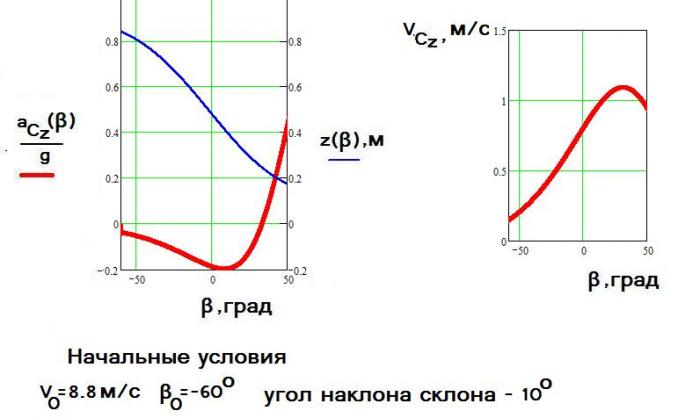
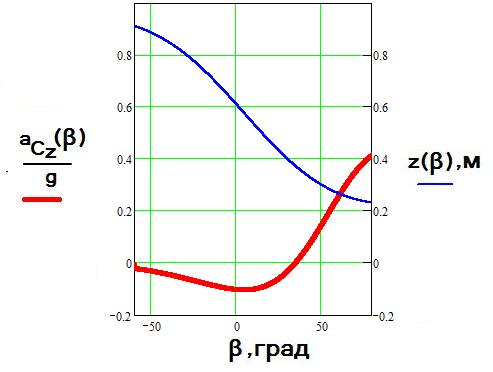
НО спортсмену требуется проехать быстро трассу, а не обеспечить равновесную дугу. Сюда надо включит переходные процессы, которые в случае отсутствия ангуляции занимаю много времени В реальности угол закантовки растет до, условно, ЛПС а потом уменьшается, в отличие от Вашей модели, в которой угол закантовки постоянно растет. Спортсмены так не едут

Поэтому я и говорю, Ваша модель практической ценности не представляет, потому что так спортсмены не едут

Собственно Nick5t5 все это уже рассмотрел в работах, к которым я Вас отсылал

Совсем недавно я со своим коллегой по статье смотрели записи с совсем свежими трансляциями Кубка мира. Слалом и гигант. Специально смотрели по поводу бокового проскальзывания. Так вот: не зафиксировали не одного чистого, без проскальзывания поворота ни у одного спортсмена ни в одной дисциплине. Все - с боковым проскальзыванием, и нигде - чисто резаного поворота! Специально смотрели!

С большой скоростью слалом.., как  раз  можно ехать, именно карвингом, т.е по  дуге, радиус которой, как в Вашей статье, меняется по  закону косинуса. Другим способом вам не удастся сделать дугу радиусом . например 5м на скорости 45км\ч Так слаломисты высоко класса и едут. А вот то, что Ваша модель не может описАть такую езду, это верно.  А интересен именно этот вариант езды, т.к"равновесными" чистыми никто не ездит. Едут либо неравновесными резаными дугами, либо равновесными, но квазирезаными, т.е когда закон косинуса не соблюдается

В спортивных лыжах, где используется боковое проскальзывание в основном для сброса избыточной скорости, чтобы не вылететь с трассы,  карвингом не ездят. Причины - Вы сами о ней сказали в одном из предыдущих постов, а именно: резаный поворот без ангуляции - наиболее быстрый из всех остальных способов, если речь идет о прохождении именно этой траектории. Все остальные - с ангуляцией, выполняются при меньшем угле наклона опорной линии, а следовательно, и с меньшей скоростью. Поворот с боковым проскальзыванием выполняется по совсем другим законам, и при этом совсем не по траектории карвингового поворота.  

Если мы заговорили о практике, то на практике  лыжники едут со скоростью , бОльшей Вашей критической скорости. Поэтому они никак не могут воспользоваться Вашей моделью с пользой для себя

С большей скоростью двигаться можно, но не карвингом, и не по рассчитанной по модели траектории.

Этот странный результат решения странной системы уравнений, которую изобрел ваш авторский коллектив, ДОЛЖЕН БЫЛ получиться именно у вас.

Вы обещали сделать эту оценку величины нормальной составляющей ускорения ЦМ вашего лыжника, но "забыли" об этом, так как она показывает очевидную неправильность вашей статьи.

Вы даже сейчас пытаетесь вводить читателей в заблуждение - Вы пишете -  А при угле до 50 градусов, судя по вашим графикам  - менее 10%, хотя из графика видно, что эта величина превышает 15%.

Я специально привожу этот график "урезанный" по 50^о . 

Также я привожу график величины проекции скорости ЦМ на ось ЗЕТ, которая по вашему предположению должна быть равна нулю.

Эта скорость очень высока для "равновесия" - она достигает почти 1м/с. Конечно, если сравнивать ее с первой космической скоростью, то она невелика.

Также обратите внимание, что координата зет ЦМ вашего лыжника изменяется почти в ТРИ РАЗА, хотя вы постулировали неизменность этой координаты во время движения вашего лыжника. Кстати, интересно, что вы не задаете начальное значение этой координаты. Оно у вас возникает "из воздуха". Вы же решаете в статье задачу Коши, а начальные условия полностью не задаете.

 

Но вопрос в другом. Как оказалось у вашего равновесного лыжника имется НАЧАЛЬНАЯ скорость движения ПО направлению к склону, которая очень быстро увеличивается.

Вы же постулировали,что в начальный момент скорость ЦМ лыжника в направлении склона РАВНА НУЛЮ.

В ваших начальных условиях начальное значение этой компоненты скорости ЦМ вообще НЕ ЗАДАЕТСЯ.

Откуда она взялась? 

 

Вы утверждали, что,по крайней мере, в начальный момент времени ваш лыжник находится в равновесии.

На самом деле, ваш лыжник ПРОЛЕТАЕТ состояние равновесия в начальный момент и в последующие моменты времени и скорость этого ПРОЛЕТА все время увеличивается. Это что же за равновесие такое? Равновесие нового типа?

 

Но раз +/- 10% для вас несущественная величина, то стоит взглянуть как будет выглядеть оценка величины нормальной составляющей ускорения ЦМ и скорости ЦМ вашего лыжника если начальную скорость увеличить на 10% до 8.8м/с.

Скорость увеличилась на 10%, а соответствующие значения ускорения больше чем в ДВА раза - до 40% от ЖЭ, а скорости - почти в полтора раза.

Вам 40% достаточно, для того, чтобы понять, что с вашей статьей все очень плохо?

 

Также не очень понятно почему вы запрещаете вашему лыжнику проехать чуть дальшепо склону - до угла бетта 90^о? Только потому, что после 50^о ваши уравнения НЕ работают?

Может вам стОит уже признать, что эти уравнения ВООБЩЕ НЕ РАБОТАЮТ?

На основании чего отказаться? На основании  того, что вы апеллируете к режимам, выходящим за пределы области существования модели? Или на основании тех ограничений, которые вы искусственно  навязываете рассматриваемой модели? И это после того, как я исчерпывающе подробно рассказал о всего двух действующих ограничениях модели (вы их почему-то игнорируете)? На основании того, что вам так хочется? Тем самым это именно вы пытаетесь ввести читателей в заблуждение, создавая у них иллюзии  некорректности приведенных решений, педалируя опять на не всеохватности  области ее существования! Позволю себе заметить, что рассматривается не "спиральный карвинг" (ваш новояз), а  моделирование конкретного резаного поворота, характеризующимися углами входа и выхода из поворота, в практике, как правило, не превышающие  45 градусов. Поэтому и интересно рассматривать те решения, которые отвечают на эти практические вопросы, а не вообще все возможные математические следствия модели, выходящие за область разумных, практических рамок. 

На этом разрешите завершить дискуссию. Считаю, что мною обсуждены все рассмотренные темы и я ответил на все поставленные вопросы! Далее - только повторение уже много раз оговоренных вопросов, что уже не  является продуктивным занятием!

Благодарю за внимание! (Если очень хочется продолжить - пишите в личку!)  

Господин Леготин.

Модель представленная в ВАШЕЙ статье  придумана вашим творческим коллективом.

Допущения также придуманы вашим творческим коллективом.

О том, что ваша модель с вашими допущениями является "реальной" имеются серьезные сомнения.

Вы говорили о том, что проверите по вашим вычислениям величину проекции ускорения ЦМ лыжника на нормальную к склону ось, которая (ось) на вашей схеме поименована как ЗЕТ.

Так как Вы об этом забыли, а я все равно загрузил ваши уравнения в ПК и  решил их для случая движения без сопротивления (который рассмотрен в вашей статье) и начальных условий в точности ИЗ ВАШЕЙ СТАТЬИ, то привожу график указанной величины проекции ускорения ЦМ лыжника на нормальную к склону ось деленной на величину ускорения свободного падения, в зависимости от угла БЕТТА, который фигурирует в других ваших графиках.

Я специально привожу относительное значение нормальной к склону составляющей ускорение ЦМ вашего модельного лыжника, чтобы можно было увидеть размер этой величины по сравнению с ЖЭ, которое, как известно равно 9.8..м/с².

Эта величина на удивление ОЧЕНЬ БОЛЬШАЯ - 40% от ЖЭ, хотя Вы доказывали здесь на форуме, что она должна быть ОЧЕНЬ МАЛЕНЬКОЙ. Из вашей статьи следует, что ваши уравнения могут быть ВЕРНЫМИ, только если эта величина ОЧЕНЬ МАЛЕНЬКАЯ.

На графике также приведена зависимость координаты Z ЦМ лыжника от угла БЕТТА.

Как видно, придуманные вами допущения о том, что величина проекции ускорения ЦМ лыжника на нормальную к склону ось является очень малой величиной НЕ соответствуют действительности.

Вы предположили, что  величина проекции ускорения ЦМ лыжника на нормальную к склону ось РАВНА НУЛЮ, благодаря этому допущению вы СИЛЬНО УПРОСТИЛИ ваши уравнения, а из решения этих уравнений следует, что величина проекции ускорения ЦМ лыжника на нормальную к склону ось СОСТАВЛЯЕТ 40% от ускорения свободного падения и больше.

Думаю, что Вам необходимо прояснить этот вопрос.

Объясните, пожалуйста, как то, что вы считали НУЛЕМ  стало после решения вашей системы величиной большей чем 4м/с²?

 

Еще раз повторю.

Величина проекции ускорения ЦМ вашего модельного лыжника на нормальную к склону ось  на удивление ОЧЕНЬ БОЛЬШАЯ - 40% от ЖЭ, хотя Вы доказывали здесь на форуме, что она должна быть ОЧЕНЬ МАЛЕНЬКОЙ.

Из вашей статьи следует, что ваши уравнения могут быть ВЕРНЫМИ, только если эта величина ОЧЕНЬ МАЛЕНЬКАЯ.

Вывод - ваши уравнения не являются верными.

Замечательный результат у вас получился! Который показывает, что, в отличие от вашей интерпретации, в моей интерпретации уравнения модели, описываемые в статье, являются правильными и вполне корректными! Причина - та же, о которой вы упомянули, а именно: при 60 градусов угла движения нормальное к склону ускорение ЦМ составляет 40% от ускорения свободного падения. А при угле до 50 градусов, судя по вашим графикам  - менее 10%, что вполне укладывается в гипотезу  о значении нормальной реакции опоры приблизительно равной весу лыжника. Таким образом, речь идет об области существовании рассмотренной модели. (А идеальных моделей описания реальных объектов не существует - рассматривается лишь различные их степени приближения). Таким образом, для рассматриваемых условий движения (скорость и угол наклона склона) это область - не превышает 50 градусов угла движения. Кстати, реальные углы движения при начале и завершении слаломного поворота, как правило, не превышают 45 градусов. Если же рассматривать менее динамичные повороты в слаломе-гиганте (соответственно радиус выреза - более 30 м ), то результаты оценки нормальных ускорений будут еще более низкими (я в этом уверен) -вы можете из посмотреть по вашим расчетам. Иными словами, "Все в порядке, господа! Это - ложная тревога!"