miron0ff

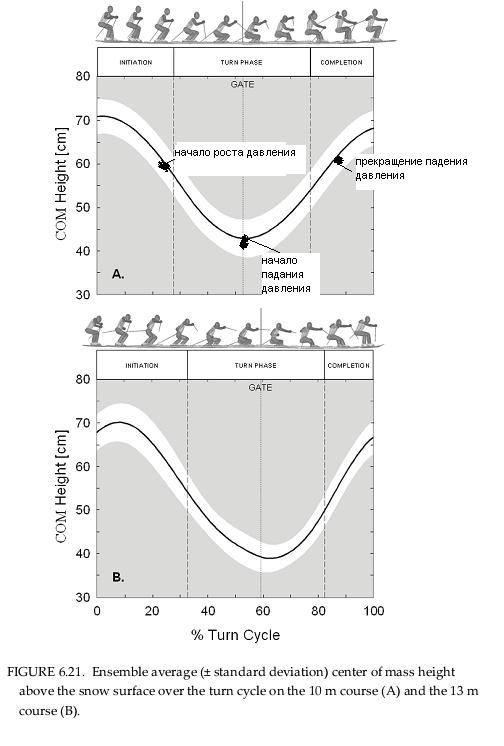
Простите, эти графики лишь отдаленно напоминают синусоиду. sin неплохо апроксимируется квадратичной и линейной функциями. Визуально они очень похожи, но производные меньше напоминают cos.

 

В гармонических колебаниях рост давления начинается вместе с началом движения вниз.

Любая физическая функция - это бесконечно гладкая функция. Такая функция локально вблизи любой точки представима степенным рядом - рядом Тэйлора.

Синус в окрестности нуля представим степенным рядом с нечетными степенями. В нем нет квадратичной составляющей.

Косинус - да. Это ряд из четных степеней.

Но если взять только первые два члена ряда для косинуса, то они противоречат "природе" косинуса. Ведь косинус это линия с изменяющейся кривизной и с явными точками перегиба, а парабола - это линия постоянной кривизны.

Поэтому к представлению периодической функции полиномом, с целью анализа ее высших производных, нужно подходить очень осторожно. Хотя, конечно же ряды для  косинуса и синуса очень быстро сходятся и радиус их сходимости - бесконечность.
 

 

Ну то была практика.

А это сухая теория. Пусть на отрезке  -e < t < e, график высоты имеет вид

 

h(t) = at³+bt²+ct+d.

 

Скорость и ускорение:

v(t) = h'(t) = 3at² +2bt+c.

 

и

 

a(t) = v'(t) = 6at +2b.

 

Пусть функция h имеет минимум в точке t=0. v(0)=0; a(0)>0. И на отрезке -e < t < e нет экстремумов.

 

0 < a(0) = 2b => 0 < b;

0 = v(0) = c.

 

Из условий минимума, на отрезке (-e, 0), 0<e скорость направлена вниз v<0, и на отрезке (0, e) скорость направлена верх 0<v.

 

3at² +2bt < 0; -e < t < 0. => 3ae²-2be < 0 => 3ae² < 2be => 3ae < 2b.

0 < 3at² +2bt; 0 < t < e. => 0 < 3ae²+2be => -3ae²-2be < 0 => -3ae² < 2be =>  -3ae < 2b.

=> -4be < 0 => снова получаем 0 < b и коэффициент a должен быть не слишком большим a < 2b/3e.

 

Если величина e мала, то e² << e. Тогда функции v и h принимают вид:

 

V(t) ~ 2bt.

A(t) ~ 6at + 2b.

 

Таким образом ускорение на отрезке (-e, e) не имеет экстремума, хотя h в точке 0 имеет минимум.

 

h в точке 0 (GATE) имеет минимум, затем максимум. В точке минимума вторая производная положительна, в точке максимума вторая производная отрицательна. Где-то между этими двумя точками вторая производная пройдет нуль. Линия графика изменит вогнутость на выпуклость. То есть после прохождения максимума вторая производная должна уменьшаться, иначе она не пройдет через нуль. Ваш анализ слишком поверхностный.

Вообще такого типа "периодические" функции очень хорошо представляются рядами Фурье. В данном случае функция четная с большой точностью. Ее ряд будет содержать основную гармонику - косинус, амплитуда которой будет много больше, чем амплитуды следующих гармоник. Вторая производная в таком представлении будет в основном + косинус. И примерно в точке GATE будет максимум. В точках 0% и 100% будут минимумы второй производной. Физически это будет означать, что ускорение цм в точке GATE направлено вверх, а в точках 0% и 100% направлено вниз. По величине они примерно одинаковы, порядка g. Поэтому в точке GATE вертикальная составляющая силы реакции склона равна примерно двойному весу лыжника в покое, а в точках 0% и 100% вертикальная составляющая силы реакции склона равна примерно нулю. Представляется, что автор работы был слаб в математике и обрабатывал данные, используя приближение полиномами. В частности он так вычислял ускорение цм. При его оснащении ему ничего не стоило применить для обработки ряды Фурье. Результаты были бы точнее особенно в указанных точках.

Так что Гойко Митич прав.