Спасибо за вопрос! Начну опять со следующего: нормальное к склону ускорение нами было принято пренебрежимо малым не для того, чтобы постулировать неизменность удаленности ЦМ системы от склона, а только для того, чтобы выразить из динамического уравнения (5) величину опорной реакции для случая, когда значение m aCz существенно меньше слагаемых правой части (квазистатическое решение). Собственно в кинематическом смысле это утверждение об отсутствии нормального к склону ускорения нигде не используется, поскольку, как Вы справедливо заметили, оно приводит к отсутствию нормальных перемещений ЦМ, что противоречит физическому смыслу поворота. Но пренебрежение в (5) левой частью позволяет получить тот результат, который в дальнейшем и обсуждается в приведенном материале. Мне кажется, что это пренебрежение вполне согласуется с тезисом о плавности движения в фазе ведения поворота, оно соответствует динамике поворота в гиганте. Исключение может представлять жесткие, динамические движения лыжника в наиболее быстро протекающих поворотах слалома., хотя численно я это не оценивал.
Спасибо за ответ.
Но на мой вопрос вы так и не ответили.
Почему при ваших компьютерных вычислениях вы не получили такого решения своей системы, которое полностью удовлентворяет всем условиям, которые вы сами же и установили - azC тождественно равно нулю и перемещения ЦМ лыжника вдоль оси Ζ не происходит?
Такое решение вашей системы существует.
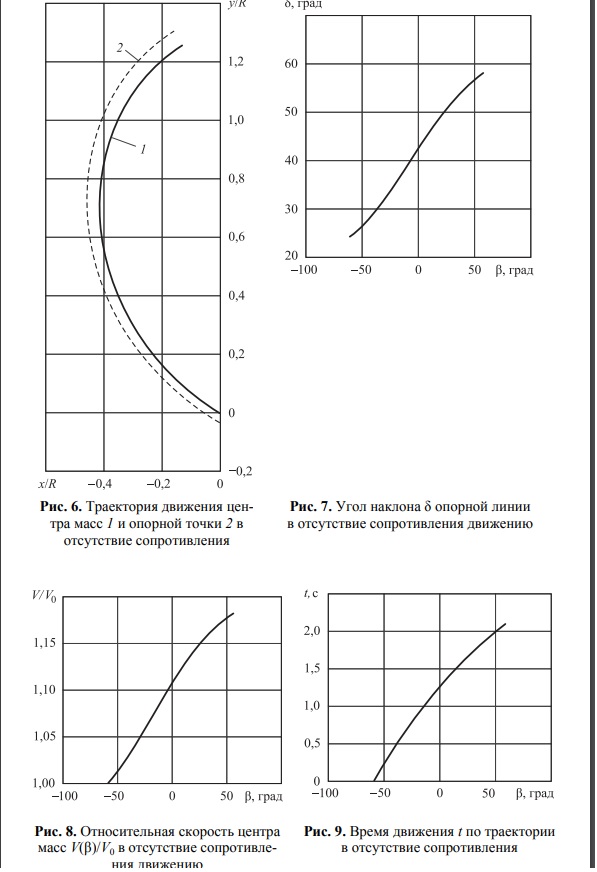
Это случай, когда лыжник во время всего движения сохраняет постоянным угол наклона опорной лини к номали к склону, что соответствует общепринятому пониманию "сохранения равновесия в повороте".
Для этого случая ваша система уравнений является правильной динамически.
Правда, скорость лыжника для реализации этого случая должна меняться экзотическим образом.
Уравнение (13) для случая постоянства угла закантовки лыж определяет однозначную связь между текущим углом β и текущей скоростью ЦМ.
Траекторией движения ЦМ будет дуга окружности, что однозначно определяет угол β и скорость даижения в каждой точке траектории.
Это решение можно получить без использования компьютера
Я его для вас привел в своем посте.
Как я понял, такого решения вашей системы уравнений вам получить не удалось.
Что касается тех решений которые приведены в статье, то они формально удовлетворяют вашей упрощенной системе уравнений.
НО для указанного в них варианта движения ЦМ лыжника, ваша система уравнений является НЕправильной.
Для формально полученного вами варианта движения ЦМ лыжника не будет выполняться ваше допущение на основании которого вы получили свою упрощенную систему уравнений из системы уравнений 2 закона Ньютона.
Абсолютно очевидно, для чего вам было нужно ваше допущение о том, что azC тождественно равно нулю и перемещения ЦМ лыжника вдоль оси Ζ не происходит.
Без этого допущения ваша система уравнений математически "не замкнута" и решить ее невозможно.
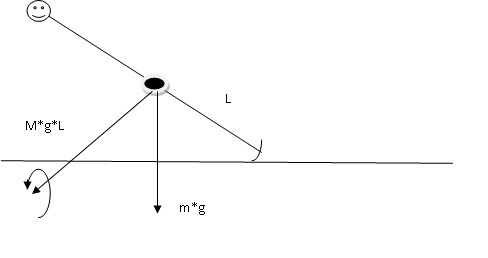
В общем случае "замкнуть" систему уравнений 2 закона Ньютона можно добавив к ней уравнение моментов относительно режущего канта монолыжи в вашей модели.
Сообщение отредактировал nick5t5: 11 November 2018 - 12:46
Это совершенно правильно. Но вы рассматриваете движение твердого тела в инерциальной системе отсчета и в этой инерциальной системе отсчета на твердое тело действует нескомпенсированный вращающий момент силы тяжести относительно опоры, оси, проходящей через лыжи.Происходит вращение вокруг этой оси, т.к угол закантовки меняется. А Вы этим вращением пренебрегли Для протяженного тела уравнений только для ЦМ недостаточно