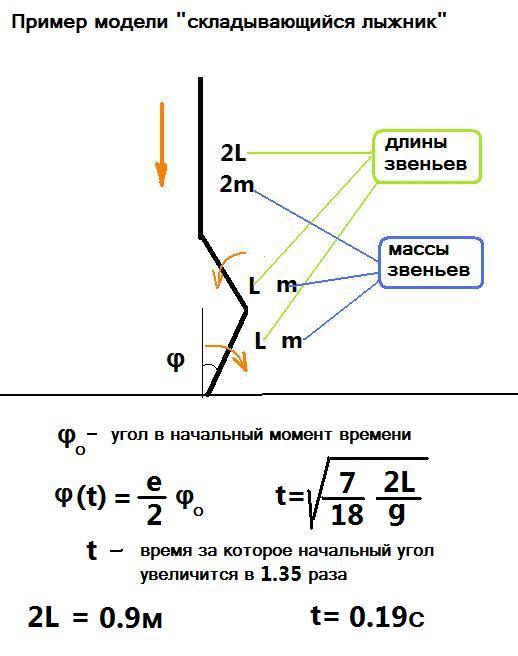
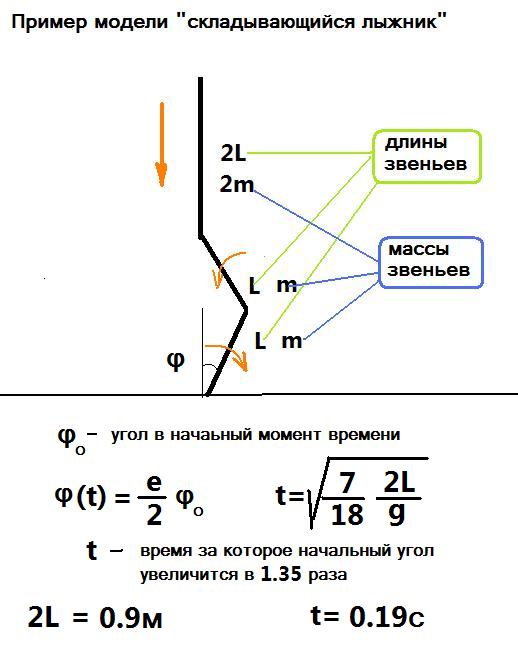
Опорная линия это отрезок опора-цм. Если лыжник не сгибается, не разгибается, то опорная линия это шест фиксированной длины. Расстояние цм до точки опоры фиксировано, скорость цм вдоль опорной линии отсутствует.
Поперечная скорость цм это скорость верхнего конца шеста, поднимающегося от склона с зафиксированным нижним концом. В каждый момент времени она направлена по касательной к описываемой окружности, и согласно школьному учебнику геометрии перпендикулярна самому шесту.
В этих условиях и до тех пор, пока опорная линия расположена между mg и mg+цбс, составляющая поперечной скорости цм вдоль mg+цбс будет иметь составляющую направленную вниз.
Вы согласны?
1.До сих пор, мы , вроде, рассматривали так называемую "разгрузку вниз",Это когда сгибаются ноги. Теперь зачем-то ВЫ рассматриваете постоянную длину шеста, хотя в контексте Ваших моделей, разгрузки вообще не должно быть, т.к расстояние от ЦМ до опоры не меняется
А ведь разгрузка есть и она вверх. Это факт фактический. Значит вариант разгрузки, обусловленный изменением расстояния ЦМ до опоры, отметаем, как негодный
2/В рассматриваемой неинерцильной системе отсчета точка опоры и ЦМ вращаются вокруг головы лыжника. На вращение опорной линии вокруг точки опоры накладывается вращение самой опорной точки. Че там в итоге получается с перпендикулярами, никто не знает
Зато известно достоверно, что проекция ЦМ на вектор mg поднимается, раз
и известно, что ЦМ движется от начального вектора mg+ЦБС к вектору mg. Этого достаточно, чтобы понять, что проекция цМ движется в верх по mg+ЦБС
Со своей разгрузкой вниз Вы впадаете в кучу противоречий, и в первую очередь в противоречие с самим Ле Мастером