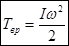ГГ не читал но если верить что ГГ так описывает поворот .
Давай рассмотрим, как ГГ описывает поворот
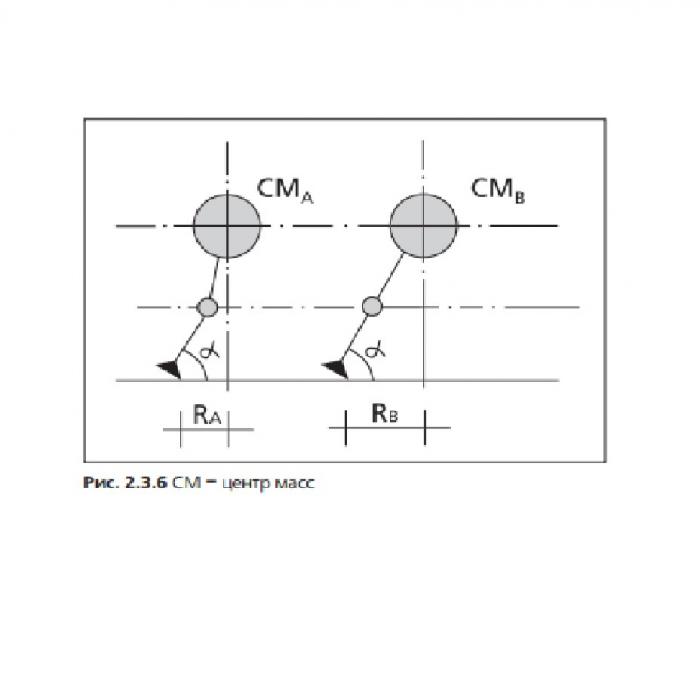
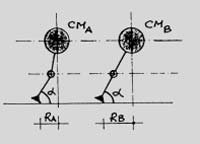
Этой картинкой ГГ старается обосновать преимущество использования заклона перед ангуляцией. Что мы видим? Едут два лыжника, одинаково закантовав лыжи, т.е по дугам одинакового радиуса. Мы же резаные повороты рассматриваем. Но ЦМ масс у лыжников отклонены от вертикали по-разному. Тот, который в заклоне, отклонился намного больше. Значит едет с заметно большей скоростью.
Если это лыжи с вырезом 27м то у одного скорость, примерно, 40км/ч, у другого, примерно, 30км/ч
Таким образом ГГ пытается нам доказать, что лыжник едущий с большей скоростью в заклоне проедет трассу быстрее, чем лыжник едущий с ангуляцией , но с меньшей скоростью. Это даже не смешно.
Но ГГ не подозревает, что этим рисунком опровергает свое же учение. Из этого рисунка видно, что все лыжники, ведущие лыжи по той же траектории, что и лыжник В, но со скоростью меньшей 40 км/ч, должны ехать с ангуляцией. Как должны ехать лыжники с бОльшей скоростью, это выходит за пределы учения ГГ никогда не ответит, что должен делать лыжник едущий по той же траектории. что и В. но с бОльшей скоростью
Анализируя этот рисунок, на основании того, что Rb>Ra, ГГ делает фантастический вывод.
"Скорость движения лыж прямо пропорциональна радиусу (смещению ). Иными словами для заданной массы, чем дальше части этой массы располагаются от оси вращения (поворота), тем больше будет энергия (импульс) создваемая при вращении(повороте).
Этого весьма примитивного приближённого объяснения (не претендующего на научность) вполне достаточно для понимания необходимости применения заклона в повороте."
Это реальный сюрр, т.к делается вывод, что надо вести ЦМ как можно дальше от центра поворота. Вероятно, центр поворота у ГГ находится там, где расположены лыжи
Похоже ГГ совсем не понимает, что лыжник старается ехать с постоянной, максимально доступной для него скоростью, и быстрее ехать не может НО из рисунка видно, что если лыжи у двух лыжников едут по одной траектории, то ЦМ намного ближе к центру поворота у В.
Сделанный выше вывод совершенно противоречит следующему выводу.
"спортсмен, режущий повороты по самой плотной траектории, проводит свой центр масс по более прямому и короткому пути от старта до финиша. Хотя одно это дает существенный выигрыш во времени, есть и другие преимущества заклона."
А уже этот вывод противоречит реальности, т.к в заклоне в трассе слалома-гиганта ЦМ перемещается по более длинной траектории, чем при ангуляции
Ну, и можно перейти к практическому совету, который дает ученикам ГГ. Для того, чтобы лыжнику В уменьшить радиус резаного поворота ГГ советует увеличить угол заклона. Но этот совет приводит к 100% падению. Из этого же рисунка следует, что лыжник должен увеличить угол закантовки дополнив это ангуляцией.
Вот и решай, читать ли тебе эту книгу. Она вся наполнена таким содержанием.
Сообщение отредактировал Гойко Митич: 09 July 2017 - 09:57




 Тема закрыта
Тема закрыта