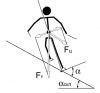
мне кажется, что она все же не приходится в среднюю точку между лыж, а смещена во внешнюю.
хм. а почему ты задал им именно такое расположение на склоне (я про углы)?
после ЛПС ЦМ будет гораздо ниже расположен, чем до ЛПС
и еще про углы (мож так нарисовано, конечно, но разве Альфа-2 больше Альфа-1?)
(сори. я только визуально могу пораспрашивать, формулы Ревкуц придет будет сравнивать)
Тань, в расчетах это не принципиально. Есть две точки - ЦМ и точка опоры, сила между которыми действует по прямой, их соединяющей.
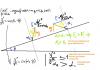
Для расчета равновесия точки треугольник векторов рисуется так: Возьмем точку в вершине поворота (касательная - линия падения)
- вертикально из ЦМ откладывается проекция силы тяжести на нормаль к склону (сила, которая давит нас к склон, это сила тяжести разложенная на скатывающую силу и силу опоры на склон, в общем, меньше чем сила тяжести, а если точно - то Fопоры=Мg*cos(a); Fскат=Mg*sin(a)
где a - угол падения склона
Задали мы к примеру перегрузку в 2g (Сила давления на канте будет зависить от массы тушки, у каждого она своя, поэтому от массы лучше вообще уйти и работать с ускорениями ее потом всегда подставить можно). Так вот, берем поперечный разрез по радиусу, и рисуем прямоугольный треугольник, у которого гипотенуза будет 2g, вертикальный катет - g*cos(a), горизонтальный - считаем по пифагору.
Корень(2^2 - cos(a)^2)
а графически - рисуем просто в масштабе приняв скажем 1g= 1см
получаем равновесное положение. но это в апексе. в верхней части дуги добавляется еще один векторок - проекция скатывающей силы на нашу плоскость сечения по нормали к склону. его величина привязана к углу поворота.
Тут запутался сам, и Вас наверное запутал. Треугольник - одинаковый по всей дуге, нижний катет состоит из векторной суммы проекции скатывающей силы и центробежки.
его общая длина не меняется, меняются эти два вектора, сумма которых постоянна.




 Тема закрыта
Тема закрыта