Не всегда так. В квазистационарных дугах, когда реакция опоры проходит через ЦМ, радиус поворота лыж больше радиуса поворота ЦМ
Я не знаю что такое "квазистационарные" дуги, да и про "стационарные" не знаю. Через какое место в "квазистационарных дугах" проходит реакция опоры, тоже не имею представления.
По-моему, сила тяжести, сила реакции опоры и их равнодействующая при поворотах на лыжах приложены (начинаются и проходят) через цм.
Радиус траектории лыж может быть больше радиуса траектории цм в некоторой точке. С этим я согласен.
Это происходит например если лыжник едет прямо (или очень большим радиусом) и активно приседает и выпрямляется. Траектория лыж практически прямая, а траектория цм имеет кривизну. При приседании - выпуклостью вниз (загрузка лыж), при выпрямлении -разгибании - выпуклостью вверх (разгрузка лыж). Максимальный радиус кривизны цм в последнем случае будет в случае отрыва лыж от снега и будет вычисляться по формуле: r=v*v/g. При скорости 36 км/ч радиус кривизны траектории цм в верхней точке, где лыжник летит горизонтально, будет равен 10 м.
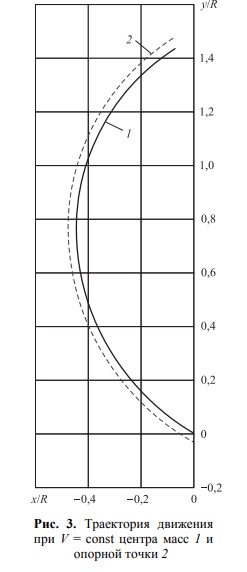
Следует отличать радиус поворота траектории от проекции траектории на склон. В этом месте перекантовки кривизна траектории лыж равна о, а кривизна траектории цм равна 0,1. Вектор кривизны траектории цм в данной точке направлен вертикально вниз, поэтому проекция его на склон является прямой линией.
При прямом спуске с выпрямлением-разгибанием траектории лыж и цм на склон совпадают и представляют из себя прямые.