Сообщений в теме: 43611

[Гойко Митич]

Митич, ты жжешь!

Сила инерции это и есть ЦБ сила ))) 

Я ж говорю, не можешь ты это произнести!

Это в неинерциальной системе отсчета, в которой эта частица покоится, т.к Fцб  =Fцс

Но мы -то рассматриваем движение по склону в инерциальной системе отсчета. В этой системе отсчета на лыжника действует  сила тяжести и реакция опоры, одной и составляющих которой является центростремительная сила, заставляющая лыжника поворачивать.

Центробежной силы, действующей на цМ лыжника , нет в ИСО

[Гойко Митич]

Даже суть то не в том, что там на глыжника действует, вопрос в другом.

Если продвигаться вперед/наружу обогнать лыжи не получится, они быстрее. Наружу/вперед увеличивает путь тулова, тк траектория удлинняется.

Нам же необходимо сократить путь тулова, изменяя траекторию движения, чтоб он, тулово, со своей медленной скоростью успело опередить быстрые лыжи. Поэтому мы двигаем тулово наперерез лыжам, сокращаем траекторию тулова, переходя через быстрые лыжи, внутрь следующего поворота.

 

Это мы лыжи все время ставим на пути ЦМ, чтобы он не ехал по прямой. А когда  мы хотим изменить направление ЦМ на противоположное, то переводим лыжи на другую сторону от прямой

Рисунки, особенно левый ни в какие ворота не лезет

Сообщение отредактировал Гойко Митич: 03 February 2019 - 15:01

[Temych]

Перепутал в конце )

Да, точно)) чем меньше погиб, тем больше радиус поворота. Спасибо что поправила )))

[Setter]

Это в неинерциальной системе отсчета, в которой эта частица покоится, т.к Fцб  =Fцс

Но мы -то рассматриваем движение по склону в инерциальной системе отсчета. В этой системе отсчета на лыжника действует  сила тяжести и реакция опоры, одной и составляющих которой является центростремительная сила, заставляющая лыжника поворачивать.

Центробежной силы, действующей на цМ лыжника , нет в ИСО

 

Митич, ты сам себе противоречишь )))

 

под  действием ЦБ  ЦМ вообще никуда не смещается, да будет тебе известно. Если полностью раскантуется, то поедет по касательной по инерции, а если лыжи загружены, то человек еще  продолжает поворачивать, хоть нога и согнута

Лыжник противодействует движению по инерции, т.е по касательной к  траектории

Ржу с тебя )))

Как уж на сковороде!

Сообщение отредактировал Setter: 03 February 2019 - 16:13

[ALEX3M]

Митич, ты сам себе противоречишь )))

 

Ржу с тебя )))

Как уж на сковороде!

 

Вовсе и не Уж, а Большой Змей!  

Но телодвижения характерные.

[Setter]

Это мы лыжи все время ставим на пути ЦМ, чтобы он не ехал по прямой. А когда  мы хотим изменить направление ЦМ на противоположное, то переводим лыжи на другую сторону от прямой

Рисунки, особенно левый ни в какие ворота не лезет

Так это и будет внутрь )))

Норм рисунки!

Тебе все не так, Жубер условно нарисовал, эти рисунки - ни в какие ворота не лезут.

Все там нормально, и у Жубера и на рисунках Кати, только они в твою схему движений не вписываются.

[Гойко Митич]

Митич, ты сам себе противоречишь )))

 

Ржу с тебя )))

Как уж на сковороде!

Я-то не противоречу  себе, а тебе надо бы освежить школьные знания. А то пока есть основания ржать на тобой.

Противодействовать движению по инерции, значит противодействовать движению по прямой. По прямой тело движется равномерно и прямолинейно, если на него не действуют силы. Подействовала сила -тело повернуло

Если бы  на лыжника действовала центробежная сила, то он бы никогда не повернул, т.к цБС=ЦСС  и они противоположно направлены и ускорение было  равным нулю. Вот как в твоем примере -тело стоит на месте Надеюсь это-хоть понимаешь?

Сообщение отредактировал Гойко Митич: 03 February 2019 - 15:28

[Гойко Митич]

Так это и будет внутрь )))

Норм рисунки!

Тебе все не так, Жубер условно нарисовал, эти рисунки - ни в какие ворота не лезут.

Все там нормально, и у Жубера и на рисунках Кати, только они в твою схему движений не вписываются.

 

Блин, что внутрь, куда внутрь?

ЦМ едет по прямой, по прямой, Карл, наружу, а лыжи его толкают внутрь

Про рисунки

1.Радиус поворота цМ не бывает в два раза меньше радиуса поворота лыж

2. Если радиус поворота лыжи больше радиуса поворота ЦМ, то центры дуг будут практически в одном месте.

Хватит или продолжить?

Лыжи в какой точке загружаются на левом?

Сообщение отредактировал Гойко Митич: 03 February 2019 - 15:25

[merry_candy]

Так это и будет внутрь )))

Норм рисунки!

Тебе все не так, Жубер условно нарисовал, эти рисунки - ни в какие ворота не лезут.

Все там нормально, и у Жубера и на рисунках Кати, только они в твою схему движений не вписываются.

Это не рисунки Кати )) И когда я их тыщу лет назад постила, я говорила, что мне они не нравятся, и нарисовала свой рисунок, самый правильный, по видео Марсика ))

[ALEX3M]

1.Радиус поворота цМ не бывает в два раза меньше радиуса поворота лыж

2. Если радиус поворота лыжи больше радиуса поворота ЦМ, то центры дуг будут практически в одном месте.

Хватит или продолжить?

Это почему?

Если дуга радиус 2 метра, а вынос внешней от ЦМ почти метр?

[bav53]

Блин, что внутрь, куда внутрь?

ЦМ едет по прямой, по прямой, Карл, наружу, а лыжи его толкают внутрь

Про рисунки

1.Радиус поворота цМ не бывает в два раза меньше радиуса поворота лыж

2. Если радиус поворота лыжи больше радиуса поворота ЦМ, то центры дуг будут практически в одном месте.

Хватит или продолжить?

Лыжи в какой точке загружаются на левом?

 

Митич, вы же прекрасно понимаете, что имеет в виду Setter. Если убрали опору на внешнюю, оставив только внутреннюю, то цбс остался, но дуга стала резко неравновесной. Поэтому цм  качнулся поперек лыж наружу на внутренней как на шесте. Зачем переводить разговор на то, кто что помнит из  школьной программы?

[ski4fun]

Эти картинки с дугами и отрезками как-то сильно далеки от реальности, две синусоиды - для траектории лыж и ЦМ, куда точнее. 

[Temych]

А вот и нет. Если убрать внешнюю, а точнее ослабить на нее опору, то никакого качания не будет, выкинет наружу или при правильном положении корпуса внутрь следующего поворота. 

 Если убрали опору на внешнюю, оставив только внутреннюю, то цбс остался, но дуга стала резко неравновесной. Поэтому цм  качнулся поперек лыж наружу на внутренней как на шесте. 

[Setter]

Я-то не противоречу  себе, а тебе надо бы освежить школьные знания. А то пока есть основания ржать на тобой.

Противодействовать движению по инерции, значит противодействовать движению по прямой. По прямой тело движется равномерно и прямолинейно, если на него не действуют силы. Подействовала сила -тело повернуло

Если бы  на лыжника действовала центробежная сила, то он бы никогда не повернул, т.к цБС=ЦСС  и они противоположно направлены и ускорение было  равным нулю. Вот как в твоем примере -тело стоит на месте Надеюсь это-хоть понимаешь?

 

Да я ж не против, можешь поржать, тем более смех продлевает жизнь, и это ХОРОШО!

НО!

В инерциальной системе не может быть силы инерции, а ты говоришь о силе инерции, ЦМ  у тебя там по инерции поедет куда то...но при этом утверждаешь, что мы находимся в ИСО, в которой действуют только силы тяжести  и реакции опоры. Какая то фигня выходит...

Но мы то на склоне находимся все же в НСО, на нас действуют силы инерции, двигаемся мы не прямолинейно и не с постоянной скоростью. Ты уж сам как то определись, где мы и что рассматриваем....

 

Фиг с ним, с этими ИСО, НСО. Тело должно обогнать лыжи, для этого нам нужно сократить траекторию тела относительно лыж. Как это сделать, если мы двигаем тело наружу поворота? Нарисуй плз...

[Maykl]

Ты отстал от жизни, есть более эффективные и менее энергозатратные приёмы для увеличения прогиба лыжи.

Да какие проблемы) Приезжай в Снежок на старты, покажешь) 

 

Как это у меня получается, пол льду и в канавах, я тебе уже показывал)

 

Сообщение отредактировал Maykl: 03 February 2019 - 16:10

[ski4fun]

Митич, вы же прекрасно понимаете, что имеет в виду Setter. Если убрали опору на внешнюю, оставив только внутреннюю, то цбс остался, но дуга стала резко неравновесной. Поэтому цм  качнулся поперек лыж наружу на внутренней как на шесте. Зачем переводить разговор на то, кто что помнит из  школьной программы?

Не надо никакой дополнительной опоры на внутреннюю ни в какой части поворота, тем более на выходе. Не делайте этого. Правильный путь - простой путь.

Сообщение отредактировал ski4fun: 03 February 2019 - 16:08

[Setter]

А вот и нет. Если убрать внешнюю, а точнее ослабить на нее опору, то никакого качания не будет, выкинет наружу или при правильном положении корпуса внутрь следующего поворота. 

Нам этого и надо.

- создать правильное положение тела

- согнуть/ослабить внешнюю

- перейти через лыжи, оставив их сзади.

Мы спереди, чего нам и требовалось добиться. 

[Setter]

Не надо никакой дополнительной опоры на внутреннюю ни в какой части поворота, тем более на выходе. Не делайте этого. Правильный путь - простой путь.

А про дополнительную опору никто и не говорит, Все что было на внутренней то и осталось

Правильный путь - простой путь. - Классно сказано!

[bav53]

Не надо никакой дополнительной опоры на внутреннюю ни в какой части поворота, тем более на выходе. Не делайте этого. Правильный путь - простой путь.

Можно и так. Вариантов хватает.

[Antry]

Даже суть то не в том, что там на глыжника действует, вопрос в другом.

Если продвигаться вперед/наружу обогнать лыжи не получится, они быстрее. Наружу/вперед увеличивает путь тулова, тк траектория удлинняется.

Нам же необходимо сократить путь тулова, изменяя траекторию движения, чтоб он, тулово, со своей медленной скоростью успело опередить быстрые лыжи. Поэтому мы двигаем тулово наперерез лыжам, сокращаем траекторию тулова, переходя через быстрые лыжи, внутрь следующего поворота.

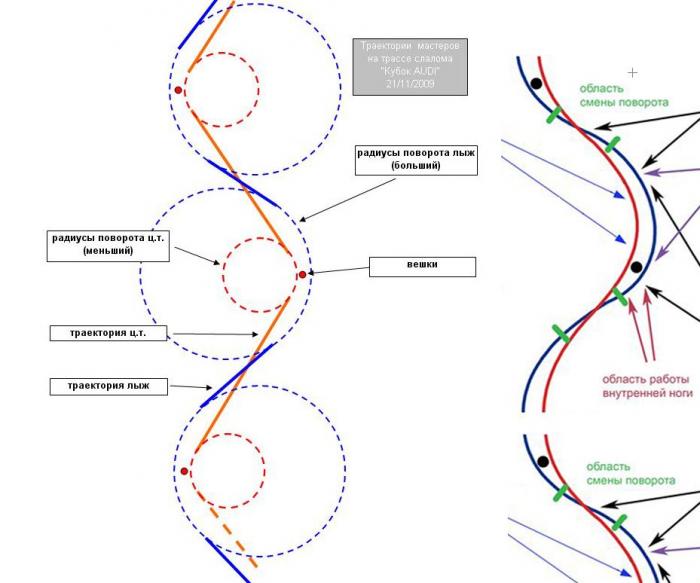
Очень странные картинки, Жубер такое не мог нарисовать.

Траектории лыж и цм понятное дело отличаются, лыжи в повороте находятся снаружи поворота, цм - внутри. Но разница в траекториях  несколько сложнее. Траектория лыж и ботинок - плоская кривая (если они не отрываются от плоского склона) переменной кривизны, а траектория цм  - это трёхмерная кривая довольно сложной формы, поскольку цм в апексе поворота находится в нижней точке, а при перекантовке - в верхней точке, да к тому же цм ещё и поворачивает по склону. Кривизна траектории цм меняется по какому-то закону в течение поворота.

Кривизна траектории лыж равна нулю при перекантовке (плоская траектория лыж  в этой точке меняет направление выпуклости) и максимальна в апексе поворота. (Кривизна траектории лыж) = 1 / (радиус поворота лыж).

Кривизна траектория цм в момент перекантовки как правило не равна нулю, а имеет выпуклость вверх, что вызывает уменьшение веса лыжника (разгрузка).  Траектория цм в повороте вообще не имеет ни одного места с нулевой кривизной, т.е. ни одного прямого участка. Кривизна не только меняется по величине, но и вектор её крутится вдоль траектории (меняет направление). Максимальную кривизну траектория цм имеет вблизи апекса поворота. В апексе поворота вектор кривизны направлен не параллельно склону, а под некоторым углом к нему. В этом же направлении направлено нормальное ускорение цм (искривляющее его траекторию) и равнодействующая (центростремительная) сила, равная произведению нормального ускорения на массу. 

Все силы и ускорения лыжника связаны с траекторией цм (не лыж).

Проекция траектории цм на плоскость склона всегда имеет меньшую кривизну (больший радиус) чем траектория лыж. В крутых слаломных поворотах лыжи идут по радиусу примерно в 1,6 раза меньшем чем цм. В пологих поворотах большого радиуса эти радиусы отличаются меньше.

Поэтому левый рисунок - это совсем неправильная нереальная схема, а правый рисунок - правильная при условии что для любой пары связанных точек (это же 2 проекции траектории одного человека) красная линия в этой точке имеет радиус  больший чем синяя. Красная линия боле пологая чем синяя для любой связанной пары точек.