Сообщений в теме: 376

[Misha_Glazov]

Механика горнолыжника-это биомеханика, нетуздесь центра масс

[Misha_Glazov]

Понял выше писал в принципе то же самое при переносе веса на внешнюю необходимо добавлять углового положения потому что масса опирающаяся на внешнюю увеличивается и ее цм смещается внутрь поворота.

biggrin.png Механика горнолыжника-это биомеханика, нетуздесь центра масс

[Antry]

 

Ну и расчет меня опять заинтересовал.

В предположении, что вращение не учитывается., то энергетический баланс выглядит просто

Vk^2=Vo^2+2*g*h/  Используя Ваши данные для изменения координаты Y, определяем перепад высот и находим, что скорость Vk в конце движения должна быть 10,7м/сек. А  из Ваших графиков следует, что она равна 9,4м/снек. Получается ошибка в 15%. На КМ с таким отставанием в скорости  человек наверное в первую сотню не попадает

Действительно, имеется сильная нестыковка для случая отсутствия трения, если взять 2 точки траектории, начальную (вета=-60) и конечную (бета=60). Радиус лыжи принят в примере расчёта без трения 12 м, начальная скорость 8 м/с, угол склона 10 градусов.

Из рисунка 6 следует, что расстояние по оси Y (вдоль лпс) равно примерно 1,23*12=14,64 м, здесь 12  - радиус лыжи. При угле склона 10 град перепад составляет 2,54 м. Потенциальная энергия на перепаде (если массу принять за 1 кг и g=9. равна около 25 Дж.

С другой стороны из рисунка 8 следует что конечная скорость равна 1,18*8=9,44, где 8 - начальная скорость. Получаем кинетическую энергию (при массе=1) примерно 12,5 Дж, т.е. в 2 раза меньше. Ровно половина энергии куда то исчезает.  В скорости это даёт ошибку примерно в 14%.

Между тем для скорости движения без трения определяющим является уравнение (3) статьи, а уравнения (4) и (5) не влияют на скорость вдоль траектории. Уравнение (3) при отсутствии трения запишется : a(tau)=g*Sin(gamma), где Sin(gamma)= Sin(alfa)*Cos(beta) - это угол склона. по которому в данном месте траектории (при данном beta) скользит тело.

Ускорение растёт до лпс, затем уменьшается, угол наклона траектории к горизонту (гамма) растёт до лпс, затем уменьшается.

Но на очень маленьком отрезке траектории для некоторого угла beta  для очень малого отрезка времени (дельта t) движение можно считать движением с одинаковым ускорением  a по наклонной плоскости с углом gamma. Задачка скольжения по наклонной плоскости решается легко и потенциальная энергия на малом отрезке в точности переходит в кинетическую.

[Legotin_S]

 

 Спасибо за ясную формулировку вопроса. Судя по большому количеству вопросов по "нестыковке с законом сохранения" понял, что на этот вопрос надо ответить серьезно. Но сначала хотелось бы отметить следующее. Вопрос об определении скорости движения при повороте прямо связан с решением дифференциального уравнения (22) при начальных условиях. Для корректного расчета движения лыжника в повороте необходимо задать значения сил сопротивления движению, т.е. сил трения и аэродинамического сопротивления, что, как уже я говорил, является крайне сложной задачей, требующей самостоятельного исследования. Без знаний сил сопротивлений остается только проиллюстрировать, как работает рассмотренная модель в самых простейших случаях изменения скорости, например, при постоянстве скорости движения, либо для случая, когда этими силами пренебрегают.  Работа была написана более полутора лет назад - пришлось залезать в старую программу расчета и искать несоответствие. Мне кажется, нашел причину (приведенная на рис.8 зависимость соответствует углу наклона склона, равному 5 градусов) Для 10 градусов вот требуемая зависимость:

 

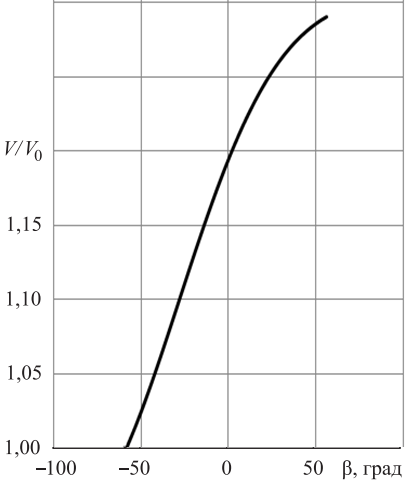
 Остальные графики не привожу из-зи их громоздкости.

Без вашего тщательного контроля и не заметил бы. Но это - уже прошлая работа. Сейчас важно описать поворот с ангуляцией, а затем и поворот с проскальзыванием. Ну и конечно постараться - без ошибок!

Сообщение отредактировал Legotin_S: 27 November 2018 - 05:51

[pretty]

 Спасибо за ясную формулировку вопроса. Судя по большому количеству вопросов по "нестыковке с законом сохранения" понял, что на этот вопрос надо ответить серьезно. Но сначала хотелось бы отметить следующее. Вопрос об определении скорости движения при повороте прямо связан с решением дифференциального уравнения (22) при начальных условиях. Для корректного расчета движения лыжника в повороте необходимо задать значения сил сопротивления движению, т.е. сил трения и аэродинамического сопротивления, что, как уже я говорил, является крайне сложной задачей, требующей самостоятельного исследования. Без знаний сил сопротивлений остается только проиллюстрировать, как работает рассмотренная модель в самых простейших случаях изменения скорости, например, при постоянстве скорости движения, либо для случая, когда этими силами пренебрегают.  Работа была написана более полутора лет назад - пришлось залезать в старую программу расчета и искать несоответствие. Мне кажется, нашел причину и вот требуемая зависимость:

 

 Остальные графики не привожу из-зи их громоздкости.

Без вашего тщательного контроля и не заметил бы. Но это - уже прошлая работа. Сейчас важно описать поворот с ангуляцией, а затем и поворот с проскальзыванием. Ну и конечно постараться - без ошибок!

ошибка осталась

Vk^2=Vo^2+2*g*h/  Используя Ваши данные для изменения координаты Y, определяем перепад высот и находим, что скорость Vk в конце движения должна быть 10,7м/сек. А  из Ваших графиков следует, что она равна в исправленном варианте

1,29*8=10,32м/сек. Получается ошибка в 3,5%.

[pretty]

для тс

есть еще одна проблема со статьей

 

 

из формулы 13 следует что для случая без трения при бетта=0 двуногий лыжник поедет точно по лпс в наклоненном состоянии

с увеличением скорости лыжник должен будет увеличивать угол закантовки и тогда он будет продолжать ехать по прямой точно по лпс

если бетта=0 то дельта однозначно связана со скоростью движения

для любой скорости от 8м/с до 10,7м/с лыжник может подобрать такой угол дельта так что угол бетта должен будет остаться нулевым

это означает движение точно по лпс и по прямой

ваши уравнения разрешают такое движение лыжнику 

если лыжник может регулировать угол наклона как вы это здесь рассказывали то он вполне может так ехать

ваша модель может творить чудеса

[Legotin_S]

для тс

есть еще одна проблема со статьей

 

 

из формулы 13 следует что для случая без трения при бетта=0 двуногий лыжник поедет точно по лпс в наклоненном состоянии

с увеличением скорости лыжник должен будет увеличивать угол закантовки и тогда он будет продолжать ехать по прямой точно по лпс

если бетта=0 то дельта однозначно связана со скоростью движения

для любой скорости от 8м/с до 10,7м/с лыжник может подобрать такой угол дельта так что угол бетта должен будет остаться нулевым

это означает движение точно по лпс и по прямой

ваши уравнения разрешают такое движение лыжнику 

если лыжник может регулировать угол наклона как вы это здесь рассказывали то он вполне может так ехать

ваша модель может творить чудеса

Да нет, конечно! Не следует смешивать разные понятия: двигаться по ЛПС и ехать по прямой. Первое - это мгновенное состояние, направление движения меняется в другой момент времени. Что касается оставшейся ошибки .3,5%, то, как я уже говорил, остальные графики тоже изменятся, поэтому расхождений не будет. 

Сообщение отредактировал Legotin_S: 27 November 2018 - 05:48

[pretty]

Да нет, конечно! Не следует смешивать разные понятия: двигаться по ЛПС и ехать по прямой. Первое - это мгновенное состояние, направление движения меняется в другой момент времени. Что касается оставшейся ошибки .3,5%, то, как я уже говорил, остальные графики тоже изменятся, поэтому расхождений не будет. 

Да нет, конечно! - это ваше высказывание к чему относится?

из ваших уравнений получается что лыжник может для данной скорости подбирать угол наклона так что угол бетта=0 в начальный и все последующие моменты времени

это означает неизменность направления движения

 

вы рассказали как ваш лыжник может регулировать угол наклона при движении по своему усмотрению

только этим вы объяснили те странные решения которые вы опубликовали в статье

 

если ваш лыжник может регулировать угол наклона при движении по своему усмотрению то он может так регулировать угол наклона что будет ехать по прямой в наклоненном положении

и это решение будет полностью удовлетворять вашим уравнениям

то есть лыжник будет ехать в равновесии

решение не более странное чем те которые вы опубликовали

 

в статье ваш лыжник падает на склон в полном равновесии и едет по криволинейной траектории

вы получили такой странный результат как решение вашей системы уравнений 

 

ваша система имеет и другие решения - лыжник падает на склон в полном равновесии и едет по прямолинейной траектории

решение странное но не более странное чем решения из статьи

Сообщение отредактировал pretty: 27 November 2018 - 11:58

[Revkuts]

в статье ваш лыжник падает на склон в полном равновесии и едет по криволинейной траектории

вы получили такой странный результат как решение вашей системы уравнений 

 

ваша система имеет и другие решения - лыжник падает на склон в полном равновесии и едет по прямолинейной траектории

решение странное но не более странное чем решения из статьи

А если у лыжника есть некая начальная скорость смещения "внутрь" поворота?

прохождение через равновесные состояния его ни замедлят, ни ускорят.

[Revkuts]

 Для корректного расчета движения лыжника в повороте необходимо задать значения сил сопротивления движению, т.е. сил трения и аэродинамического сопротивления, что, как уже я говорил, является крайне сложной задачей, требующей самостоятельного исследования. Без знаний сил сопротивлений остается только проиллюстрировать, как работает рассмотренная модель в самых простейших случаях изменения скорости, например, при постоянстве скорости движения, либо для случая, когда этими силами пренебрегают. 

Мне кажется можно пойти на допустимое упрощение.

Ведь при реальном катании скорость в ритмичном коридоре стабилизируется примерно уже на 3 - 4 повороте.

 

Получается, что с момента стабилизации средней скорости остается некое ее пульсирование в каждой дуге, с ускорением и замедлением, а в точке сопряжения дуг скорость постоянна от цикла поворота к циклу.

 

Энергия перепада высоты + мышечная работа при ее наличии поглощается силой трения полностью.

Энергия перепада считается легко, мышечная работа думаю за 200 джоулей не выйдет.

 

Среднюю скорость в зависимости от развода ворот можно приблизительно прикинуть по времени прохождения трассы...

 

Длину дуги - тоже.

 

Давление на опору в каждый момент времени описано  пусть условиями равновесия.

 

Получается, что можно попробовать используя некие эмпирические данные, вроде  скорость в сопряжении 60 км/ч на склоне с уклоном 10 градусов при радиусе дуги 20 метров и отклонении от линии ската при сопряжении 30 градусов вычислить как длину дуги, перепад и  "размазанную" по дуге энергию.

 

То есть попробовать расчитать "эффективый" коэффициент трения от обратного и применять его затем в модели.

 

Если это автоматизировать, то есть считать траекторию движения на компьютере с малым шагом, то алгоритм будет сходящимся, за некоторое количество итераций под начальные условия можно подогнать удовлетворяющий им коэффициент трения.

 

Просчитали с маленьким - скорость на выходе больше. Просчитали с увеличенным - скорость на выходе меньше, делим пополам... повторяем, а достигнув требуемой точности прекращаем. 

 

Причем заодно просчитывается интересный вопрос, по которому мы спорили с Митичем:

где происходит потеря скорости, а где ее рост при пульсации во время поворота?

 

Я думал, что скорость растет в ЛПС, где скатывающая сила больше, а Митич утверждал, что наоборот, ибо там апекс поворота и максимум закантовки, центробежки и соответственно трения... А может быть есть удачные сочетания одного и другого, взаимно компенсирующие ускорение по дуге.

 

Прошу прощения за отсутствие формул. Математику забыл еще в школе, а достаточно глубоко и не знал.

Сообщение отредактировал Revkuts: 27 November 2018 - 19:13

[pretty]

А если у лыжника есть некая начальная скорость смещения "внутрь" поворота?

прохождение через равновесные состояния его ни замедлят, ни ускорят.

нужно определиться с понятием - равновесное состояние

любое состояние механической системы описывается уравнениями динамики

в любом уравнении есть правая и левая части 

их соединяет знак равенства

справедливость уравнений динамики означает что их правые и левые части находятся в балансе или в равновесии в любой момент времени

так можно сказать что лыжник всегда находится в равновесии

может это и есть динамическое равновесие о котором все говорят?

в другой теме обсуждается понятие - динамический равновесный баланс

быть может - это следующая ступень эволиции?

Сообщение отредактировал pretty: 28 November 2018 - 10:59

[Legotin_S]

Мне кажется можно пойти на допустимое упрощение.

Прошу прощения за отсутствие формул. Математику забыл еще в школе, а достаточно глубоко и не знал.

Спасибо за желание помочь!

[Antry]

Хочу спросить про силы сопротивления.

Их всего две - сила трения скольжения о снег  F ск и сила противления воздуха Fсопр.

Эти обе силы направлены против вектора скорости, в отрицательном направлении тау. Они обе реально тормозят и действуют очень похоже. Нет особой разницы кататься против сильного ветра или кататься например по свежевыпавшему снегу на несмазанных лыжах, Разогнаться в обоих случаях не получиться и удовольствие будет ниже среднего. Сила трения скольжения приложена  к лыжам, сила сопротивления воздуха в целом к тушке, но ведь это не очень принципиально с т.з. катания и с т.з. модели ? (Принципиально отличаются только способы уменьшения этих сил). Почему нельзя объединить эти 2 силы в одну и считать их обе приложенными к ц.т. ? На точность модели по-моему это не особо повлияет. особенно на фоне последующих допущений. 

Эта суммарная сила сопротивления  будет проекцией реакции опоры на ось тау: R тау = F ск + F сопр. Остальные две проекции силы реакции будут R n перпендикулярно лыжам и R z перпендикулярно склону. При этом не нужен будет угол дзета и система сил будет более наглядная. На решения это по-идее никак не должно повлиять ?

[Legotin_S]

Хочу спросить про силы сопротивления.

Их всего две - сила трения скольжения о снег  F ск и сила противления воздуха Fсопр.

Эти обе силы направлены против вектора скорости, в отрицательном направлении тау. Они обе реально тормозят и действуют очень похоже. Нет особой разницы кататься против сильного ветра или кататься например по свежевыпавшему снегу на несмазанных лыжах, Разогнаться в обоих случаях не получиться и удовольствие будет ниже среднего. Сила трения скольжения приложена  к лыжам, сила сопротивления воздуха в целом к тушке, но ведь это не очень принципиально с т.з. катания и с т.з. модели ? (Принципиально отличаются только способы уменьшения этих сил). Почему нельзя объединить эти 2 силы в одну и считать их обе приложенными к ц.т. ? На точность модели по-моему это не особо повлияет. особенно на фоне последующих допущений. 

Эта суммарная сила сопротивления  будет проекцией реакции опоры на ось тау: R тау = F ск + F сопр. Остальные две проекции силы реакции будут R n перпендикулярно лыжам и R z перпендикулярно склону. При этом не нужен будет угол дзета и система сил будет более наглядная. На решения это по-идее никак не должно повлиять ?

Можно и так - дело вкуса. Однако эти силы приложены к разным точкам - к лыжам и к центру аэродинамического сопротивления. При переносе их в ЦМ необходимо добавлять моменты этих сил относительно ЦМ. Эти моменты - направлены в разные стороны: момент силы трения стремится заставить "клюнуть" лыжника вперед, момент силы аэродинамического сопротивления - опрокинуть назад (если ЦАС выше ЦМ). Если учитывать в качестве основной силу трения, то для  компенсации момента этой силы нужно отклонить ЦМ назад. Отсюда и появляется угол дзета. В случае наличия бокового скольжения - дело сложнее выглядит.

[Alex_63]

biggrin.png Механика горнолыжника-это биомеханика, нетуздесь центра масс

 

Центра нет никогда био не био давит каждый кубический мм массы, причем все они давят под разными углами но в итоге получается суммарный вектор давления в лыжу, который и определяет будет лыжа резать или проскальзывать и вектор  этот в каждый момент будет определятся тем, где находится цм биомассы о которой Вы говорите. Цм этой биомассы при переносе веса на внешнюю будет смещаться внутрь поворота и соответственно вектор давления в лыжу будет выполаживаться а значит его надо вертикализировать (иначе лыжа будет проскальзывать) а для этого необходимо добавить ангуляции.

[pretty]

обнаружилась научная статья 2004г где такие уравнения уже  решались

и успешно были решены

получено целое многообразие (поверхность) решений

затронут вопрос ограничения скорости сверху

https://arxiv.org/ab...ysics/0310086v3

есть даже ссылка на аналогичную работу 1996г

 

в вашей статье нет ссылок на эти древние работы

это у вас ренесанс?

Сообщение отредактировал pretty: 30 November 2018 - 12:22

[Antry]

обнаружилась научная статья 2004г где такие уравнения уже  решались

и успешно были решены

получено целое многообразие (поверхность) решений

затронут вопрос ограничения скорости сверху

https://arxiv.org/ab...ysics/0310086v3

есть даже ссылка на аналогичную работу 1996г

 

в вашей статье нет ссылок на эти древние работы

это у вас ренесанс?

Большое спасибо pretti, что она откопала научную статью по механике горных лыж.  Наука ведь не может развиваться в отдельно взятой стране, необходимо общение и чтение статей коллег из разных стран. За это же большое спасибо Нику5т5 что он знакомит нас с диссертациями на тему горных лыж. А где бы мы ещё про это почитали ? Особенно интересны различные экспериментальные результаты, пусть даже они имеют в основном "социальный" характер (как справедливо заметил один лыжник на этом форуме), т.е спорт поддерживает университеты. Ну и пусть поддерживает, формулы и университетские эксперименты скорей всего не улучшат реального катания. но они интересны сами по себе. В конце концов как сказал один мудрец, "ничего нет полезнее хорошей теории" или  "правильная теория может когда-нибудь пригодиться" или что-то похожее в этом роде.

Фрайбургский университет - старейший в Германии и почитать статью его сотрудников конечно интересно.

Не вникал до конца и очень глубоко, но вот первое впечатление.  

Во-первых, инерциальная система координат выбрана достаточно примитивно, оси  - горизонально (вдоль и поперёк лпс) и вертикально. Отсюда появляются все эти линейные матрицы, которых можно было бы избежать, проявив мало-мальски смекалку и выбрав "естественные" инерциальные оси для лыж - вдоль лыж, поперёк лыж и перпендикулярно склону. Половина косинусов и синусов бы ушла.

Во-вторых, 3/4 статьи (вплоть до формулы(19) авторы раскладывают силу тяжести на плоскость склона по разным направлениям. Всё это можно сделать гораздо проще при разумном выборе инерциальных осей.

В-третьих, силы трения о снег и о воздух вообще не рассматриваются. Это всё равно что рассчитывать прыжок с парашютом без учёта воздуха. Полезно с т.з. проверки математической модели.

И наконец в-четвёртых (и это очень серьёзное упущение) авторы в главе 2,5  и на рисунке 5 вводят в расчёт центробежную силу инерции, ни словом не обмолвившись о той неинерциальной системе координат, в которую они внезапно перешли и без которой центробежная сила инерции не существует. Это нехорошо и непонятно. В их системе координат хyz никакой центробежной силы не существует, а другую систему они не описали.

Ну и (PS) в пятых, не прилично рассуждать о динамике тела, ни разу не упомянув и не использовав второй закон Ньютона.

В общем 3/4 статьи сила тяжести раскладывается по разным проекциям, а в оставшейся части появляется зачем-то  другая система отсчёта  (о которой не сказано ни слова) и соответственно нетрадиционное (очень странное) решение.

 

Интересно так же было бы почитать отзыв об этой статье Леготина.

Сообщение отредактировал Antry: 30 November 2018 - 21:43

[Antry]

Можно и так - дело вкуса. Однако эти силы приложены к разным точкам - к лыжам и к центру аэродинамического сопротивления. При переносе их в ЦМ необходимо добавлять моменты этих сил относительно ЦМ. Эти моменты - направлены в разные стороны: момент силы трения стремится заставить "клюнуть" лыжника вперед, момент силы аэродинамического сопротивления - опрокинуть назад (если ЦАС выше ЦМ). Если учитывать в качестве основной силу трения, то для  компенсации момента этой силы нужно отклонить ЦМ назад. Отсюда и появляется угол дзета. В случае наличия бокового скольжения - дело сложнее выглядит.

Согласен про моменты, да и трудно не согласиться. Но ведь уравнения 1-2-3 справедливы и для точки, в которой нет моментов ?

Для точки tg(дзета)=Rtau / Rn ?

[Legotin_S]

Согласен про моменты, да и трудно не согласиться. Но ведь уравнения 1-2-3 справедливы и для точки, в которой нет моментов ?

Для точки tg(дзета)=Rtau / Rn ?

Конечно. Мы используем т.н."Кенигову" систему, где рассматривается движение системы со скоростью ее ЦМ плюс вращение системы вокруг ЦМ. Поскольку анализ динамической задачи позволил через принятые допущения не рассматривать динамику вращения, фактически система свелась к движению ЦМ. Именно поэтому в упомянутых уравнениях нет моментов.  По второму Вашему вопросу ( tg(дзета)) - так и есть, но только не для "точки", а для компонентов опорной реакции системы. 

Что касается статьи, то честно скажу - вижу ее первый раз, не знал о ее существовании. Надо с ней разбираться по-существу. Со временем, к сожалению, туговато, но сделаю это обязательно и обязательно поделюсь своим впечатлением, если интерес к теме не пропадет. 

А вообще, я совершенно не ожидал проявление такого интереса к вопросу о механике горных лыж, дискуссия была интересной и весьма полезной, в чем я бесконечно всем участникам форума благодарен несмотря на разные, подчас весьма "острые" постановки вопросов. Мне сложилось впечатление, что этим форумом тему не исчерпать и она может претендовать на присутствие на сайте в качестве постоянной рубрики.  

Сообщение отредактировал Legotin_S: 02 December 2018 - 12:32

[Antry]

Попробую немного размочить сухую тему механики поворотов на наклонной плоскости.

По-моему у этих расчётов есть реальное применение. Самое простое, где можно применить довольно простую математическую модель поворотов и расчёта траектории - это помощь в постановке трасс, т.е. математическое моделирование расстановки вешек на конкретном склоне.

Насколько я понимаю на своём любительском уровне, постановка даже простой любительской трассы на коротком склоне - это нетривиальная творческая задача. Постановка трассы - это своего рода искусство, которое доступно опытным тренерам, но и у них иногда бывают ошибки, когда трасса оказывается слишком сложной для тех, для кого предназначена, или наоборот слишком простой. Здесь много факторов - прежде всего уровень лыжников, потом состояние склона, его уклон и перепады. особенно если это незнакомый склон. В постановке есть небольшая доля политики, поскольку если на соревнованиях ставит трассу свой тренер, то наверное это хорошо для его подопечных, но не всегда это срабатывает.

Трасса слалома по-моему самое сложное для математического моделирования, хотя скорости небольшие и всё видно на несколько ворот вперёд и назад. Но верю, что компьютер (смартфон) вполне сможет помочь расставить вешки на конкретном склоне на уровне среднего тренера и при средних условиях для любителей.

Трассу скоростного спуска (насколько я слышал) ставят на конкретном склоне по одному  варианту из года в год, возможно с минимальными изменениями. Не знаю, применяется ли мат моделирование при проектировании новых склонов под трассу для скоростного спуска. Новых склонов для этого вроде бы не появляется, но у старых иногда слегка меняется профиль, поскольку меняются условия скольжения и лыжи. Мат моделирование траектории спуска в этом деле вполне может помочь.

Если бы существовала такая мат модель трасс скоростного спуска, то если в неё заложить профиль например трассы Штрайф, то думаю, что вердикт компьютера был бы "не пригодна к перепрофилированию и эксплуатации в современных условиях". (Это моё оценочное суждение). Но ведь не только наука вообще, но и бизнес (в частности Китцбюэля) требуют жертв ?

Может существовать цель создания мат. модели помощи тренеру в  расстановке вешек  в зависимости от профиля склона, условий скольжения и уровня лыжников.