Сообщений в теме: 373

[rzuev]

Интересное выпрямление перед поворотом.

Только теперь оно не по лыжам делается, а с вращение бедра и тела над лыжей внутрь поворота.

стопэ, в твоей механике это разминка голени, откуда тут взялось бедро?

 

а вообще, этот прием абсолютно ситуативный и скорее следствие реализуемой траектории, нежели чем технический приём, который нужно тренировать

 

нанешь пытаться удерживать корпус в долину и не отрывать лыжи в транзите - само получится

Сообщение отредактировал rzuev: 06 January 2024 - 23:57

[Alex62]

Интересное выпрямление перед поворотом.

Только теперь оно не по лыжам делается, а с вращение бедра и тела над лыжей внутрь поворота. Тогда лыжа встаёт на нижний кант и начинает поворачивать до ЛПС.

В твоём исполнении нога в колене выпрямляется и кантовать не может

Выпрямляется она на лпс, где тело уже лежит в повороте.

[mcureenab]

стопэ, в твоей механике это разминка голени, откуда тут взялось бедро?

Лыжа под бедром вращается, бедро над лыжей вращается. Закон относительности движения.


Между бедром и лыжей голень разминается

[mcureenab]

Выпрямляется она на лпс, где тело уже лежит в повороте.

Смотри какой там на видосике положняк.

На крутом да. До ЛПС есть смысл вращаться за ЛПС и там упираться и поворачивать, чтобы успевать и не разносило.

[mcureenab]

нанешь пытаться удерживать корпус в долину и не отрывать лыжи в транзите - само получится

Однокурсник так и делает. Корпус в долину. Не подпрыгивает. Но распрямляет ногу и пихает лыжу в упор перед собой за ЛПС, а не позади до ЛПС.

Само на лыжах не получается, а без лыж делает.

[rzuev]

нужно не забывать про стейлоу

[miron0ff]

 

Ну то была практика.

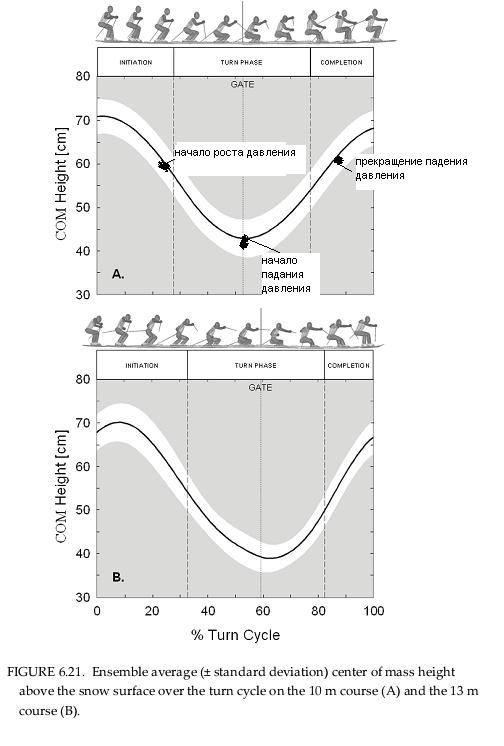
А это сухая теория. Пусть на отрезке  -e < t < e, график высоты имеет вид

 

h(t) = at³+bt²+ct+d.

 

Скорость и ускорение:

v(t) = h'(t) = 3at² +2bt+c.

 

и

 

a(t) = v'(t) = 6at +2b.

 

Пусть функция h имеет минимум в точке t=0. v(0)=0; a(0)>0. И на отрезке -e < t < e нет экстремумов.

 

0 < a(0) = 2b => 0 < b;

0 = v(0) = c.

 

Из условий минимума, на отрезке (-e, 0), 0<e скорость направлена вниз v<0, и на отрезке (0, e) скорость направлена верх 0<v.

 

3at² +2bt < 0; -e < t < 0. => 3ae²-2be < 0 => 3ae² < 2be => 3ae < 2b.

0 < 3at² +2bt; 0 < t < e. => 0 < 3ae²+2be => -3ae²-2be < 0 => -3ae² < 2be =>  -3ae < 2b.

=> -4be < 0 => снова получаем 0 < b и коэффициент a должен быть не слишком большим a < 2b/3e.

 

Если величина e мала, то e² << e. Тогда функции v и h принимают вид:

 

V(t) ~ 2bt.

A(t) ~ 6at + 2b.

 

Таким образом ускорение на отрезке (-e, e) не имеет экстремума, хотя h в точке 0 имеет минимум.

 

h в точке 0 (GATE) имеет минимум, затем максимум. В точке минимума вторая производная положительна, в точке максимума вторая производная отрицательна. Где-то между этими двумя точками вторая производная пройдет нуль. Линия графика изменит вогнутость на выпуклость. То есть после прохождения максимума вторая производная должна уменьшаться, иначе она не пройдет через нуль. Ваш анализ слишком поверхностный.

Вообще такого типа "периодические" функции очень хорошо представляются рядами Фурье. В данном случае функция четная с большой точностью. Ее ряд будет содержать основную гармонику - косинус, амплитуда которой будет много больше, чем амплитуды следующих гармоник. Вторая производная в таком представлении будет в основном + косинус. И примерно в точке GATE будет максимум. В точках 0% и 100% будут минимумы второй производной. Физически это будет означать, что ускорение цм в точке GATE направлено вверх, а в точках 0% и 100% направлено вниз. По величине они примерно одинаковы, порядка g. Поэтому в точке GATE вертикальная составляющая силы реакции склона равна примерно двойному весу лыжника в покое, а в точках 0% и 100% вертикальная составляющая силы реакции склона равна примерно нулю. Представляется, что автор работы был слаб в математике и обрабатывал данные, используя приближение полиномами. В частности он так вычислял ускорение цм. При его оснащении ему ничего не стоило применить для обработки ряды Фурье. Результаты были бы точнее особенно в указанных точках.

Так что Гойко Митич прав.

 

Сообщение отредактировал miron0ff: 07 January 2024 - 15:47

[Очень ленивый]

Ну вот, совсем другое дело. Как пелена с глаз упала…

[potap_69]

нужно не забывать про стейлоу

Роман, вот беда с английским - скажи, что имеется ввиду по-русски.

[demon75]

Роман, вот беда с английским - скажи, что имеется ввиду по-русски.

 

Оставайся ниже

стой ниже

движение вниз телом в долину

подтягивай ноги снизу 

сгруппируйся

Сел встал

 

Интересно самому

честно не знаю 

Сообщение отредактировал demon75: 07 January 2024 - 16:03

[miron0ff]

Простите, эти графики лишь отдаленно напоминают синусоиду. sin неплохо апроксимируется квадратичной и линейной функциями. Визуально они очень похожи, но производные меньше напоминают cos.

 

В гармонических колебаниях рост давления начинается вместе с началом движения вниз.

Любая физическая функция - это бесконечно гладкая функция. Такая функция локально вблизи любой точки представима степенным рядом - рядом Тэйлора.

Синус в окрестности нуля представим степенным рядом с нечетными степенями. В нем нет квадратичной составляющей.

Косинус - да. Это ряд из четных степеней.

Но если взять только первые два члена ряда для косинуса, то они противоречат "природе" косинуса. Ведь косинус это линия с изменяющейся кривизной и с явными точками перегиба, а парабола - это линия постоянной кривизны.

Поэтому к представлению периодической функции полиномом, с целью анализа ее высших производных, нужно подходить очень осторожно. Хотя, конечно же ряды для  косинуса и синуса очень быстро сходятся и радиус их сходимости - бесконечность.
 

[potap_69]

Оставайся ниже

стой ниже

движение вниз телом в долину

подтягивай ноги снизу 

сгруппируйся

Сел встал

 

Интересно самому

честно не знаю 

У меня, как у "классика" с этим беда.)))

[mcureenab]

. Ее ряд будет содержать основную гармонику - косинус, амплитуда которой будет много больше, чем амплитуды следующих гармоник. 

 

 

мы смотрим на эффекты следующего порядка, а ты их просто выкинул. Это грубая ошибка

 

Вот второй член ряда разложения прямоугольной функции порождает 3 экстремума в полупериоде.

[mcureenab]

h в точке 0 (GATE) имеет минимум, затем максимум. В точке минимума вторая производная положительна, в точке максимума вторая производная отрицательна. Где-то между этими двумя точками вторая производная пройдет нуль. Линия графика изменит вогнутость на выпуклость. То есть после прохождения максимума вторая производная должна уменьшаться, иначе она не пройдет через нуль. Ваш анализ слишком поверхностный.

.

 

 

Я рассматриваю ограниченный интервал, где h принимает только минимум. Естественно, за пределами интервала кубическая функция будет сильно отличаться от гармонической.

 

После прохождения экстремума вторая производная где-то должна поменять знак. А уменьшаться/увеличиваться вторая производная может начать и до и после и в точке экстремума. Что я продемонстрировал.

[mcureenab]

Роман, вот беда с английским - скажи, что имеется ввиду по-русски.

 

 

Это наверное из серии видосиков

 

https://youtu.be/gTv...nA2kPvpbfieDNIt

 

 

Крис флексит и в транзите стоит низко, а Сара разгибается, и стоит высоко

[Папалыжник]

Оставайся ниже

стой ниже

движение вниз телом в долину

подтягивай ноги снизу 

сгруппируйся

Сел встал

 

Интересно самому

честно не знаю 

 

В транзите на горшке тренируйте https://youtu.be/v8Y...Z5xtuae6z5NBug9

[demon75]

В транзите на горшке тренируйте https://youtu.be/v8Y...Z5xtuae6z5NBug9

Щас)))) от этой кукарачи избавлялись хрен знает сколько времени) хоть как упражнение или разовый тех приём хорошо.

[Папалыжник]

Щас)))) от этой кукарачи избавлялись хрен знает сколько времени) хоть как упражнение или разовый тех приём хорошо.

 

Зря, сейчас этот разовый техприём является многомногоразовым у всех "топов". Вот ещё два варианта. Можете понаблюдать отличия. https://youtu.be/F73...ZYXMJrlkw3hKMB6 https://youtu.be/FuD...OBUSZnby9FkOiGP

[Гойко Митич]

Это наверное из серии видосиков

 

https://youtu.be/gTv...nA2kPvpbfieDNIt

 

 

Крис флексит и в транзите стоит низко, а Сара разгибается, и стоит высоко

 

А Крис не катается как Одерматт, потому, что в транзите стоит низко.

 Автор, похоже, не разбирается,  почему топ-спортсмены в одних случаях сгибают ноги в транзите, в других - разгибают . Сомнительный совет - советовать чайнику  сгибать ноги в транзите   

Сообщение отредактировал Гойко Митич: 07 January 2024 - 18:51

[nick5t5]

мы смотрим на эффекты следующего порядка, а ты их просто выкинул. Это грубая ошибка

 

Вот второй член ряда разложения прямоугольной функции порождает 3 экстремума в полупериоде.

Синий график как две капли воды похож на график Степаныча)) Ты хоть понимаешь то, что тебе написали? Человек говорил о гладкой функции. Вот как Степаныч привел график Рейда.

Взял бы для примера функцию Дирихле. Все сразу бы поняли что ты очень крут.