Сообщений в теме: 3020

[mcureenab]

Набор заблуждений.

 

При каких условиях внешняя сила РО не направлена в ЦМ?

[ALEX3M]

При каких условиях внешняя сила РО не направлена в ЦМ?

При ускоренном движении цм вверх или вниз.

[ALEX3M]

Это все давно заметили. Из жалости молчали

Зато не болею Вождизмом в запущенной форме ) 

[mcureenab]

При ускоренном движении цм вверх или вниз.

 

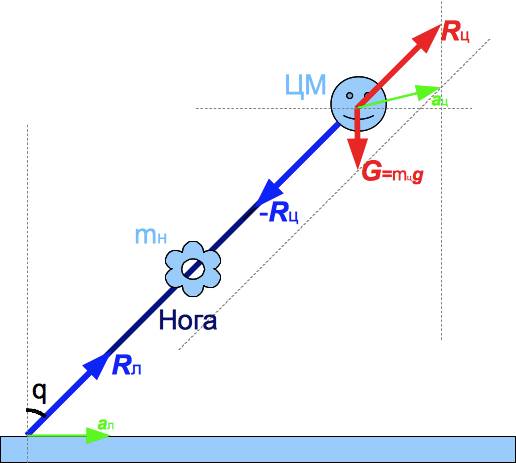
Ускоренное движение вверх. А R в ЦМ смотрит.

[Antry]

Можно попытаться оценить энергию вращения лыжника по сравнению с энергией его перемещения как единого целого (цм).

Теорема Кёнига (википедия)

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

T=T1+T2   где T -полная кинетическая энергия системы, T1 -кинетическая энергия движения центра масс, T2 - оттносительная кинетическая энергия системы (относительно центра масс).

При рассмотрении движения абсолютно твёрдого тела  обычно кинетическую энергию записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=m*v*v/2+I*w*w/2

Здесь m -масса тела, v -скорость центра масс, w, I -угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс.

 

Подсчитаем энергию движения цм и энергию вращения вокруг цм.

энергия движения цм:    m=100  V=10     m*v*v/2=5000 Дж

энергия вращения вокруг центра масс: пусть корпус будет цилиндром с радиусом 0,25 м тогда момент инерции I=m*r*r/2=3.13

угловая скорость вращения : пусть лыжник делает очень закрытый поворот на 90 градусов (1.5 радиана) за 2 секунды и при этом поворачивает корпус вслед за лыжами (это нормально при любительском  карвинге средними дугами).

скорость вращения w=1.5/2=0.75 рад/с  Энергия вращения   3,13*0,75*0,75/2=0,88 Дж

энергией вращения лыжника вокруг собственной оси можно пренебречь по сравнению с энергией его движением вниз по склону.

 

Можно рассматривать вращение лыжника как движение массы в повороте. Тогда его момент инерции приближённо равен (мат. точка) m*R*R где R - мгновенный радиус поворота. Подставляя в формулу энергии вращения получаем m*R*R*w*w/2=m*v*v/2, т.е кинетическую энергию движения цм с линейной скоростью v.

Вывод: не забивать себе голову разными вращениями, их энергия пренебрежимо мала по сравнению с энергией движения лыжника вниз по склону, определяемой перепадом высоты и потерями на скольжение и сопротивление воздуха. 

[mcureenab]

Энергия тут не очень важна. Важны моменты импульсов. Чуть неправильно подкрутился на трамплине и приземлишься на спину.

[mcureenab]

В повороте осаживает на корму. Это тоже следствие сохранения момента импульса.

[Гойко Митич]

Подсчитаем энергию движения цм и энергию вращения вокруг цм.

энергия движения цм:    m=100  V=10     m*v*v/2=5000 Дж

энергия вращения вокруг центра масс: пусть корпус будет цилиндром с радиусом 0,25 м тогда момент инерции I=m*r*r/2=3.13

угловая скорость вращения : пусть лыжник делает очень закрытый поворот на 90 градусов (1.5 радиана) за 2 секунды и при этом поворачивает корпус вслед за лыжами (это нормально при любительском  карвинге средними дугами).

 

"Пусть"... Лыжник в повороте -это не цилиндр вращающийся вокруг своей продольной оси. ОН наклонен. Если угол закантовки равен 60 градусам, то проекция роста лыжника на плоскость склона составляет 0,86  роста. Вот и посчитай какова энергия вращения лыжника  вокруг поперечной оси, если его реальный рост равен 2м.. НЕ забудь про  10кг лыж с ботинками находящимися примерно на расстоянии 0,8м от центра масс.

А угловую скорость вычисляй просто, используя известные экспериментальные данные: V=11.5м/сек, радиус поворота равен 5м. Т.е угловая скорость равна 2,3/сек

[ALEX3M]

Ускоренное движение вверх. А R в ЦМ смотрит.

Что за " a л" зеленая?
Я за вашей дискуссией не слежу.

[mcureenab]

Что за " a л" зеленая?
Я за вашей дискуссией не слежу.

Ускорение лыжи. Вся конструкция должна ускоряться вправо, чтобы нога не вращалась в плоскости диаграммы.

[ALEX3M]

Ускорение лыжи. Вся конструкция должна ускоряться вправо, чтобы нога не вращалась в плоскости диаграммы.

Лыжа ускоряется поперёк канта внутрь поворота?

[mcureenab]

Лыжа ускоряется поперёк канта внутрь поворота?

Да. Это же ЦС ускорение.

Сообщение отредактировал mcureenab: 01 February 2020 - 12:01

[ALEX3M]

Да. Это же ЦС ускорение.

 А по какой причине вертикальная составляющая реакции опоры больше, чем mg?

[mcureenab]

А по какой причине вертикальная составляющая реакции опоры больше, чем mg?

Видимо, лыжник так захотел. Он может управлять величиной aл меняя угол закантовки и радиус поворота.

Ноге некуда деватся и она толкает ЦМ (эффект шеста). В ответ ЦМ ускоряется и увеличивается Rц.

[rzuev]

Т.е это уже процесс раскантовки через шест.

[ALEX3M]

Видимо, лыжник так захотел. Он может управлять величиной aл меняя угол закантовки и радиус поворота.

Ноге некуда деватся и она толкает ЦМ (эффект шеста). В ответ ЦМ ускоряется и увеличивается Rц.

Хотелось бы услышать всю цепочку,последовательно, а не только начало и конец.
Если лыжник уменьшает r поворота, своими действиями по увеличению угла закантовки, что меняется в первую очередь, а что уже меняется как следствие?
Если уменьшить радиус поворота, то в первую очередь изменяется ЦСУ.
И сила РО изменит и величину, а главное- и направление.
Она будет направлена ближе к горизонту, и пройдет ниже ЦМ.
Что и является причиной возникновения вращающего момента.
Который при неподвижной точке опоры вызовет подьем ЦМ и увеличение нормального давления на склон.

Сообщение отредактировал ALEX3M: 01 February 2020 - 13:12

[mcureenab]

Т.е это уже процесс раскантовки через шест.

 

На диаграмме изображен неравновесный поворот. Изменение угла q зависит от вертикальной скорости ЦМ. В начале поворота ЦМ движется вниз и q увеличивается. После апекса ЦМ движется вверх и q уменьшается.

 

И ещё замечу, что q это угол инклинации, а не закантовки. После апекса q уменьшается, а закантовка может оставаться прежней и даже увеличиваться.

[ALEX3M]

На диаграмме изображен неравновесный поворот. Изменение угла q зависит от вертикальной скорости ЦМ. В начале поворота ЦМ движется вниз и q увеличивается. После апекса ЦМ движется вверх и q уменьшается.

 

И ещё замечу, что q это угол инклинации, а не закантовки. После апекса q уменьшается, а закантовка может оставаться прежней и даже увеличиваться.

При такой постановке вопроса никаких закономерностей не найти.
И не понять ничего.

[mcureenab]

Хотелось бы услышать всю цепочку,последовательно, а не только начало и конец.
Если лыжник уменьшает r поворота, своими действиями по увеличению угла закантовки, что меняется в первую очередь, а что уже меняется как следствие?
.

Причинно-следственные связи в динамике не предусмотрены. Тут как бы вопрос стоит о том, относительно каких переменных нужно решать уравнение движения. Если нам известен график движения лыжи, то остальные величины мы находим от этого графика.

Нам могут быть известны графики большего числа величин, чем требуется. Тогда вопрос будет стоять, имеют ли уравнения движения решение.

[mcureenab]

При такой постановке вопроса никаких закономерностей не найти.
И не понять ничего.

Закономерности известны. Начальные условия не все заданы для того чтобы понять увеличивается q или уменьшается.