to Nik:
Вы должны согласиться, что формула зависимости радиуса поворота от угла закантовки и от выреза лыж, в которую Вы свято верите, в общем случае не верна, а может быть принята в качестве аппроксимации с точностью 10-15 % в диапазоне углов закантовки 20-60 градусов, т.е вблизи угла в 40 градусов. Эта формула: r=R*cos(alfa) или r=R*Sin(90-alfa) где r - радиус поворота R - радиус выреза. На этой формуле Вы основываете свои научные статьи во всём диапазоне углов закантовки и делаете соответствующие выводы.
Лучше всего опровергает эту формулу диссертация, в которой сделан эксперимент по её подтверждению. Наглядно видно, что после углов в 60 градусов эта формула не работает. При малых углах она тоже не работает. Это же очевидно. Автор диссертации вдавливает плоско лежащую лыжу в снег и получает отпечаток лыжи - радиус выреза и из этого делает вывод, что плоская лыжа поедет по радиусу её выреза. Плоская незакантованная лыжа всегда едет прямо вниз, это подтвердит любой впервые вставший на лыжи, а чтобы лыжа поворачивала по своему радиусу, нужно поучиться кататься пару-тройку лет чтобы закантовать её градусов на 20-30 на нормальной скорости. Вот тогда она поедет по своему радиусу.
Поэтому если вы берёте за основу своей теории поведение математической лыжи по этой формуле, не нужно делать выводов про реальное катание при углах закантовки меньше 20 град и больше 60.
Я бы при создании разных теорий и моделей пользовался бы законами Ньютона и делал бы какие-то обоснованные ограничения для получения каких-то решений.
Прикольно так же читать эпиграф к Вашей первой статье от Ю. Данилочкина про центробежные силы в повороте. При всём уважении к Данилочкину как к лыжнику, на уроки физики ему ходить было некогда - он тренировался в разных странах. Он как смог передал свои ощущения от настоящего хорошего поворота. Про центробежные силы наверно он слышал от своих тренеров, которым тоже некогда было ходить на физику. Никто им не рассказал, что центробежной силы на самом деле не существует.
Вы упустили главное - результаты, изложенные в моей статье применимы ко всем типам поворотов, поэтому Ваша озабоченность формулой косинуса не очень понятна.
Более того, ее активно используют авторы статьи, которую Вы здесь активно продвигали. Вы с ними этот вопрос обсуждали?
Далее
Я Вам уже на нечто подобное отвечал, но Вы, очевидно, мои ответы не читаете, что несколько НЕ вежливо с Вашей стороны.
Повторю мой ответ:
Я Вам, Antry, очень рекомендую изучить труд Федервольфа, так как ситуация с ним несколько сложнее, чем вы это изложили.
Федервольф в своей работе, фактически, подтвердил формулу Howe ДЛЯ МЯГКОГО СНЕГА и для ДВИЖУЩЕЙСЯ В НЕМ ЛЫЖИ. Для жесткого склона формулу даже проверять не нужно - это ОБЩЕПРИЗНАНО.
Он не столько измерял радиус лыжи вдавленный в снег, сколько производил расчеты радиуса изгиба "реальной" лыжи в движении, который он вычислял методом конечных элементов, используя данные по свойствам снега(мягкий,тверже и тд), полученные в его натурном эксперименте по вдавливанию лыжи в снег, и сравнивал эти вычисленные по методу конечных элементов радиусы лыжи, движущейся по "реальному" склону, с учетом наличия на них креплений и лыжника, с формулой Howe.
При этом, Федервольф исходил из "пещерных", абсолютно ложных знаний о направлении силы реакции опоры в динамическом повороте.
Что и приводит к некоторым расхождениям его расчетов с формулой на больших углах закантовки.
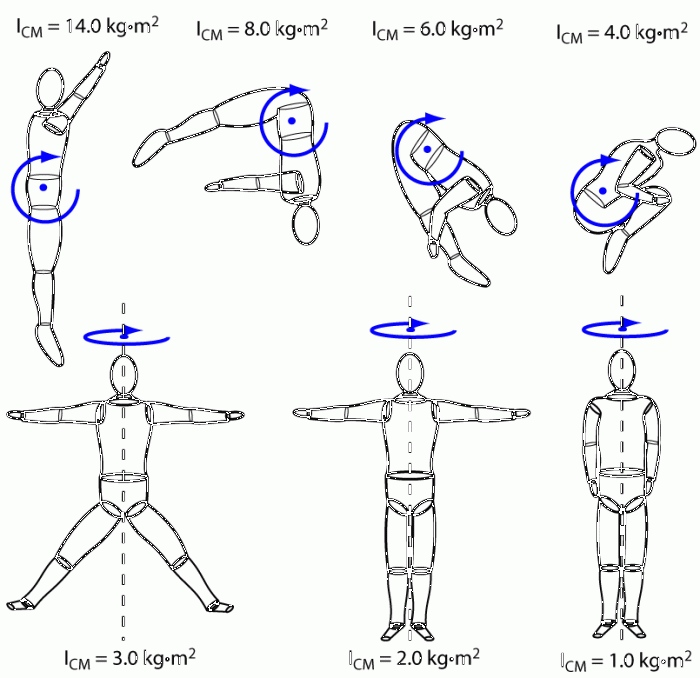
Очевидно что Федерольф предполагал, что лыжник давит на лыжу в направлении указанном на рисунке, что неверно. Правильное направление указано ниже желтой стрелкой.
При этом на его стенде на углах около 70о уже ничего путного он получить не мог, так как мягкий снег лыжу не держал.
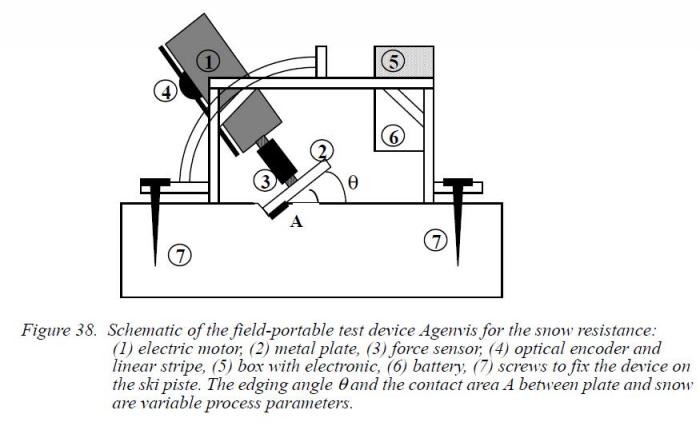
Но на практике даже для топов КМ, которые кантуют лыжи свыше 70о угол между направлением давления в лыжу и нормалью к склону НЕ превышает 60о, поэтому то что он получил хорошее совпадение при своих расчетах для 60о является реальным результатом для 70о.
Также расчеты он производил для силы давления не больше 1400н, но реальные значения превышают 3000н. (данные Рейда)
По данным Федерольфа при увеличении силы давления расчетный радиус для мягкого снега существенно уменьшается
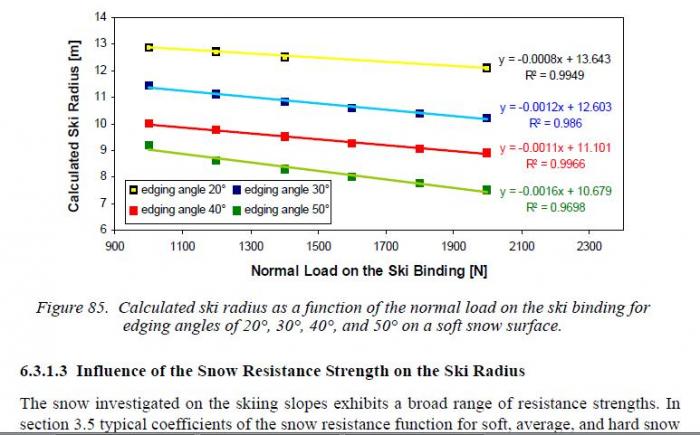
Как видно из его же данных увеличение давления с 1400н до 3000н уменьшит расчетный радиус лыжи на 2-3м. А тогда его данные с точностью лягут кривую, расчитанную по формуле. Можете сами убедиться.
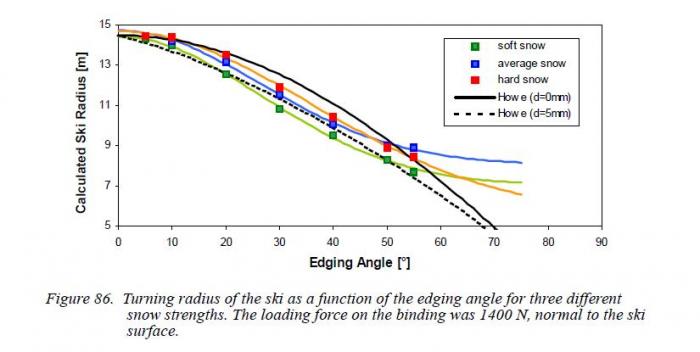
Учитывая результаты Рейда о максимальной инклинации ЦМ лыжника в повороте в 50 с небольшим градусов при максимальном угле закантовки в более чем 70о, расчеты Федерольфа охватывают весь диапазон углов закантовки, которые используют спортсмены и его расчеты полностью подтверждают формулу Howe ДЛЯ МЯГКОГО СНЕГА
Для ОЧЕНЬ твердого склона эта формула работает ВСЕГДА и переходит в формулу косинуса.
Прошу Вас провести дискуссию на тему формулы косинуса с Ривлиным и его соавторами, а до этого меня по данному вопросу более не беспокоить.
Сообщение отредактировал nick5t5: 24 May 2018 - 14:11
, прошлым летом разбирали "шпиндель" я пришел к выводу что нужно заменить пихание лыж в бок,пихание себя
